км/мин.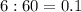
км/мин.
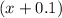км/мин.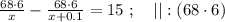
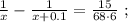
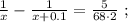
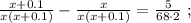
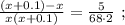
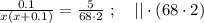
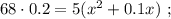
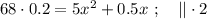
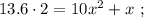
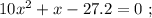
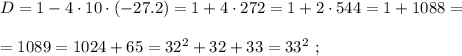
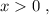так, как это скорость,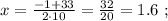
y=-2(x-1)^2
y=-2(x^2-2x+1)
y=-2x^2+4x-2
f(x)=-2x^2+4x-2
График - парабола, ветви вниз, т.к. коэффициент при x^2 отрицательный,
a=-2.
Точка вершины параболы (1;0): x=-b/2a=-4/2*-2=-4/-4=1;
y=-2*1+4*1-2=-4+4=0
Пересечение с осью У, при х=0: -2*0+4*0-2=-2 - точка пересечения (0;-2).
Точки пересечения с осью Х, при y=0:
-2x^2+4x-2=0 |2
-x^2+2x-1=0
D=2^2-4*(-1)*(-1)=0 Уравнение имеет один корень
х=(-2+0)/-2=1
График пересекается с осью Х в точке (1;0), т.е. вершина параболы лежит на оси 0Х.
График во вложении
f'(x)=3x^2-4x
f(a)=-1-2+3=0
f'(a)=3+4=7
y=f(a)+f'(a)(x-a)=0+7(x+1)=7x+7