Найдите корни уравнения:
1) 7+2x²=2(x+1)(x+3)
постепенно раскрываем скобки
7+2х²=2(х²+3х+х+3)
7+2х²=2(х²+(3х+х)+3)
7+2х²=2(х²+4х+3)
7+2х²=2х²+8х+6
перенесём всё в правую часть и приравняем уравнение к нулю, при этом не забываем сменить знаки на противоположные
2х²+8х+6-7-2х²=0
группируем или приводим подобные члены
(2х²-2х²)+8х+(6-7)=0
8х-1=0
8х=1
х=1:8
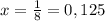
____________________________________________________
7+2·(0,125)²=2(0,125+1)(0,125+3) (это проверка)
7,03125=2·1,125·3,125
7,03125=7,03125
2) (y+4)(y+1)=y-(y-2)(2-y)
постепенно раскрываем скобки
у²+у+4у+4=y-(2y-y²-4+2y)
у²+у+4у+4=y-(-y²+(2y+2y)-4)
у²+у+4у+4=y-(-y²+4y-4)
у²+у+4у+4=y+y²-4y+4
перенесём всё в левую часть и приравняем уравнение к нулю, при этом не забываем сменить знаки на противоположные
у²+у+4у+4-y-y²+4y-4=0
группируем или приводим подобные члены
(у²-y²)+(у+4у-y+4y)+(4-4)=0
8у=0
у=0
(0+4)(0+1)=0-(0-2)(2-0)
4·1=0-(-2·2)
4=0-(-4)
4=0+4
4=4
2) Задача
Обозначим кроликов "к", а фазанов "ф"
у кроликов по 4 лапы, а у фазанов 2
согласно данным условия задачи составляем систему уравнениий:
4к+2ф=100 (1)
к+ф=36 (2)
к=36-ф
4(36-ф)+2ф=100
144-4ф+2ф=100
144-2ф=100
2ф=144-100
2ф=44
ф=44:2
ф=22 (шт.) - фазаны.
к=36-ф=36-22=14 (шт.) - кролики.
ответ: В клетке находятся 14 кроликов и 22 фазана.
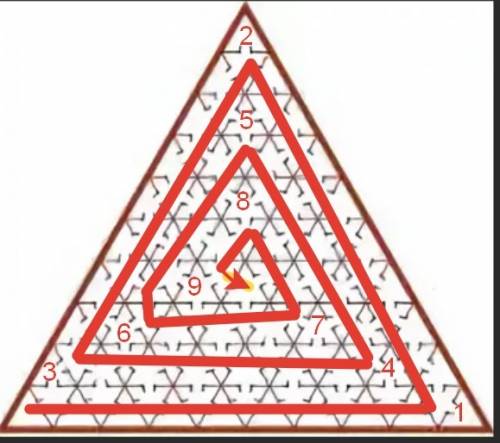
Для того, чтобы выяснить наибольшее число залов, которые можно обойти, не заходя ни в какой зал дважды, нужно правильно раскрасить замок - треугольник. Раскрашиваем в шахматном порядке. Тогда путь по залам - это граф, с вершинами в центрах залов и ребрами - проходами между залами. Видно, ни одно ребро не соединяет вершины одного цвета.
Если начать раскрашивать с первого нижнего углового треугольника в порядке: 1 красим, один - нет, то сумму незакрашенных треугольников можно вычислить по формуле сцммы 1-х n-членов арифметической прогрессии:
а₁=1 (второй верхний ряд треугольников сверху:
а₂=9 (десятый ряд треугольников)
Всего незакрашеные треугольники есть в 9-и рядах, вершина - закрашена)
S₉=(1+9)/2*9=5*9=45 незакрашенных треугольников - залов, значит можно посетить не более 45 незакрашенных залов.
Тогда маршрут может проходить не более, чем по 45+1 закрашенным залам: А - незакрашенный треугольник;
В - закрашенный треугольник.
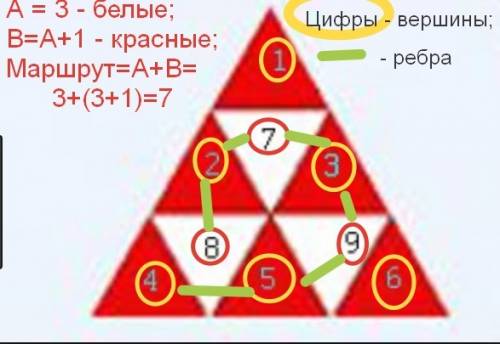
Маршрут=А+В=А+(А+1)=45+45+1
Маршрут = 91 зал
Во вложении 1 - маршрут, который начинается в нижнем левом треугольнике и, продолжаясь по спирали, заканчивается в среднем закрашенном треугольнике, в четвёртом снизу ряду.
Залы, в которые не надо заходить, иначе придется посетить один зал дважды, отмечены чифрами от 1 до 9 по маршруту движения.
Для наглядности, во вложении 2, пример, подтверждающий формулу, рассмотрен на маленьком треугольнике, разделенном на 9 маленьких.