1) В таблице.
2)Координаты точки пересечения графиком оси Ох (0,5; 0);
Координаты точки пересечения графиком оси Оу (0; -2).
3)у= -3 при х= -0,25
4)Согласно графика, в 4 четверти лежит точка (0,3; -0,8)
Объяснение:
Задана функция y=4x-2
1) Постройте график функции.
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблица:
х -1 0 1
у -6 -2 2
2) Найдите координаты точек с пересечения графика с осями координат.
а)график пересекает ось Ох при у=0.
y=4x-2
у=0
0=4х-2
-4х= -2
х= -2/-4
х= 0,5
Координаты точки пересечения графиком оси Ох (0,5; 0)
б)график пересекает ось Оу при х=0.
y=4x-2
х=0
у=0-2
у= -2
Координаты точки пересечения графиком оси Оу (0; -2)
3) Определите аргумент функции, если её значение ровно -3.
Найти значение х.
у= -3
y=4x-2
-3=4х-2
-4х= -2+3
-4х=1
х=1/-4
х= -0,25
у= -3 при х= -0,25
4) Укажите координаты точки на графике, которая лежит в 4 четверти(любой одной).
Согласно графика, в 4 четверти лежит точка (0,3; -0,8)
1. Выполните действие:
1.) 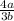 ;
;
2.) 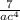 ;
;
3.) 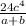 ;
;
4.) 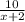 .
.
2. Упростите выражение:
1.) 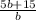 ;
;
2.) 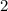 .
.
3. Представьте в виде степени с основанием a выражение:
1.) 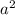 ;
;
2.)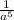 ;
;
3.) 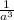 .
.
Объяснение:
1. Выполните действие:
1.) Сокращаем - 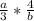 ; Умножаем -
; Умножаем - 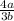 .
.
2.) Сокращаем - 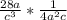 ; Ещё раз сокращаем -
; Ещё раз сокращаем - 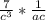 ; Умножаем -
; Умножаем - 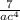 .
.
3.) Находим множитель и сокращаем - 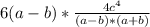 ; Сокращаем -
; Сокращаем - 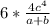 ; Считаем -
; Считаем - 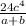 .
.
4.) Находим множитель и делем - 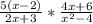 ; Раскладываем на множители -
; Раскладываем на множители - 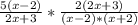 ; Сокращаем -
; Сокращаем - 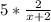 ; Считаем -
; Считаем - 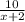 .
.
2. Упростите выражение:
1.) Раскладываем на множители - 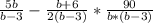 ; Сокращаем -
; Сокращаем - 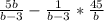 ; Умножаем -
; Умножаем - 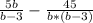 ; Ищем наименьший общий знаменатель -
; Ищем наименьший общий знаменатель - 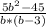 ; Раскладываем на множители -
; Раскладываем на множители - 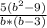 ;Ещё раз раскладываем на множители -
;Ещё раз раскладываем на множители - 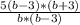 ; Сокращаем -
; Сокращаем - 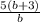 ; Раскрываем скобки домножая на 5 -
; Раскрываем скобки домножая на 5 - 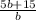 .
.
2.) Ищем наименьший общий знаменатель - 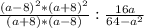 ; Раскладываем на множители -
; Раскладываем на множители - 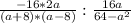 ; Считаем -
; Считаем - 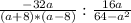 ; Считаем и делим -
; Считаем и делим - 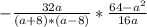 ; Ищем множители и сокращаем -
; Ищем множители и сокращаем - 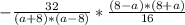 ; Выносим за скобки минус и сокращаем -
; Выносим за скобки минус и сокращаем - 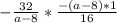 ; Сокращаем -
; Сокращаем - 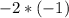 ; Умножаем -
; Умножаем - 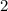 .
.
3. Представьте в виде степени с основанием a выражение:
1.) Считаем - 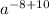 ; Считаем ещё раз -
; Считаем ещё раз - 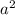 .
.
2.) Считаем - 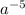 ; Представляем в виде положительной степени -
; Представляем в виде положительной степени - 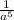 .
.
3.) Упрощаем - 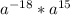 ; Считаем -
; Считаем - 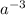 ; Представляем в виде положительной степен -
; Представляем в виде положительной степен - 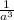 .
.
б) 10! = 1*2*3*4*5*6*7*8*9=362880
Понять данный алгоритм не трудно,он всегда используется в подобных задачках =)