![1)2y=3-1,5x \\ y= \frac{1,5(2-x)}{2} \\ y=0,75(2-x) \\ \left[\begin{array}{ccc}x&0&2\\y&1,5&0\end{array}\right] \\2)6y=-x \\y= \frac{-x}{6} \\ \left[\begin{array}{ccc}x&0&6\\y&0&-1\end{array}\right] \\3)0,5y=1+x \\y= \frac{1+x}{0,5} \\ \left[\begin{array}{ccc}x&0&1\\y&2&4\end{array}\right] \\5)y= \frac{6}{1,5} =4](/tpl/images/0256/8294/8cdd4.png)
Доказать тождество:
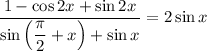
1. Определим область допустимых значений.
1.1. Выражение слева имеет смысл, если его знаменатель не равен нулю:
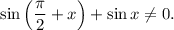
1.2. Используя формулу приведения 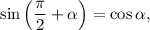 получаем:
получаем:
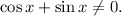
1.3. Умножим обе части на 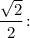
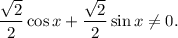
1.4. Поскольку 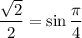 и
и 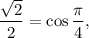 то получаем:
то получаем:
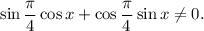
1.5. Используя формулу синуса суммы 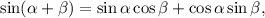 получаем:
получаем:
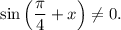
1.6. Так как 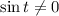 для
для 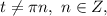 то:
то:
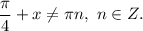
1.7. Перенесём 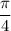 в правую часть, изменив знак на противоположный:
в правую часть, изменив знак на противоположный:
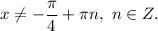
2. Докажем данное тождество, работая с левой частью равенства.
2.1. Преобразуем данное выражение, применив формулу косинуса двойного угла 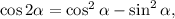 синуса двойного угла
синуса двойного угла 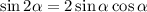 и формулу приведения
и формулу приведения 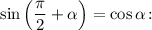
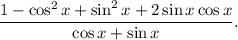
2.2. Замечаем в числителе следствие из основного тригонометрического тождества 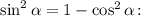
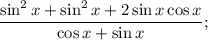
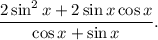
2.3. Вынесем в числителе общий множитель 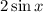 за скобки:
за скобки:
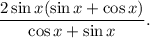
2.4. Сокращаем дробь на 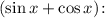
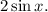
Тождество доказано.
ответ: 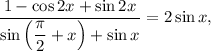 если
если 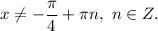
Пометка. Пункт под нахождением области допустимых значений не является обязательным при доказательстве тождества.