1) Для начала введу события, соответствующие попаданиям в мишень при 1, 2, 3.4, 5 выстрелах. Это события A1,A2,A3,A4,A5 соответственно.
2). Изветсно, что вероятность попадания в мишень при выстреле =0.8. У каждого из пяти событий существует два исхода - попадание и промах. Все исходы приму за 1. Тогда вероятность промаха при каждом выстреле равна 1 - 0.8 = 0.2.
3)Теперь введу новое событие - B, в которое входят события, при которых произошло попадание. По условию - это события A1,A2,A3. Два последних события не входят потому, что в них биатлонист промахнулся. Тогда
P(A1) = 0.8, P(A2) = 0.8, P(A3) = 0.8, P(A4) = 0.2, P(A5) = 0.2. Поскольку каждое событие не зависит одно от другого(каждое наступает в любом случае), то я применяю правило умножение вероятностей.
0.8 * 0.8 * 0.8 * 0.2 * 0.2 = 0.02048≈0.02. Задача решена )). Надеюсь, что я понятно решение изложил )
а) n-ый член геометрической прогрессии ищется по формуле:
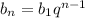
Тогда пятый член этой прогрессии равен:

б) Аналогично по формуле n-го члена геом. прогрессии вычисляем девятый член прогрессии:
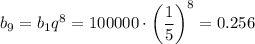
в) Сумма первых n членов геометрической прогрессии ищется по следующей формуле:
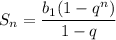
Тогда сумма первых восьми членов этой прогрессии равна:

г) Аналогично с в) по формуле суммы n первых членов геометрической прогрессии вычисляем сумму первых пяти членов этой прогрессии:
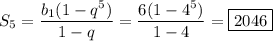
д) Предполагается, что нужно найти сумму бесконечно убывающей геометрической прогрессии:

Тогда
А) -36; - 12; -4;
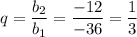
Сумма бесконечно уб. г.п. 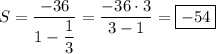
Б) 
Сумма бесконечно убывающей геометрической прогрессии:
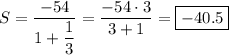
e) используя n-ый член геометрической прогрессии, рассмотрим пятый член этой прогрессии:
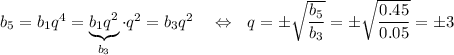
Так как по условию q>0, то q=3
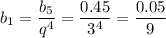
Сумма первых восьми членов этой прогрессии равна:

это IV четверть где cosα>0 и sinα<0
значит cosα=¹²/₁₃
найти tg(π/4-α)
решение: