Первая мастерская должна была сшить 160 костюмов, а вторая на 25% меньше. т.е. вторая должна сшить 160-0,25*160=120 костюмов.
вторая шила по х костюмов/день и работала 120/х дней, а первая х+10 костюмов/день и работала 160/(х+10) дней.
первая справилась на 2 дня раньше, а второй понадобились дополнительные 2 дня.
значит,
160/(х+10)+2=120/х-2
160/(х+10) - 120/х= -4
(160х-120х-1200)/х(х+10)= -4
(40х-1200)/(х2+10х)= -4
х2+10х=-10х+300
х2+20х-300=0
х=10; -30.
нам подходит только х=10.
значит, вторая мастерская шила по 10 костюмов в день.
проверяем: вторая по 10 кост/день, первая по 10+10=20 кост/день.
первая справилась за 160/20=8 дней, вторая за 120/10=12 дней.
12-8=4. разница в 4 дня. значит, срок был 10 дней, но первая справилась на 2 дня раньше(8 дней), а второй понадобились дополнительные 2 дня
(12 дней).
Дано уравнение cosx=1/(1- tgx).
сosx*(1 - tgx) = 1.
сosx - сosx*tgx = 1.
Заменим tgx = sinx/cosx,
сosx - сosx*( sinx/cosx) = 1.
cosx – sinx = 1.
Заменим sinx = √(1 – cos²x)
cosx - √(1 – cos²x) = 1.
Перенесём корень вправо, а 1 влево и возведём обе части в квадрат.
cos²x – 2cosx + 1 = 1 – cos²x,
2 cos²x – 2cosx = 0,
2cosx(cosx - 1) = 0.
Имеем 2 решения: cosx = 0 и cosx = 1.
Находим значения х:
x = arc cos 0 отбрасываем, так как при этом функция тангенса не имеет определения.
x = arc cos(1) = 2πn, n ∈ Z.
ответ: в заданном промежутке имеется 3 корня уравнения
-2π, 0, 2π.
.

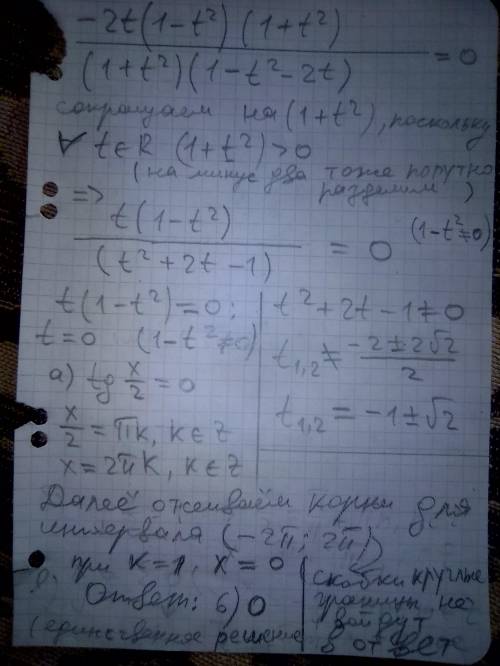

Пусть х костюмов шила вторая мастерская в день, тогда х + 10 костюмов шила первая мастерская.
160 - 160*0,25 = 120 костюмовы должна сшить вторая мастерская. По условию известно, что первая мастерская закончила работу на 2 дня раньше, а второй понадобилось еще 2 дня, следовательно получаем уравнение:
120/х - 160/(х+10) = 4
120(х+10) - 160х = 4х(х+10)
4х² + 40х = 120х + 1200 - 160х
4х² + 80х - 1200 = 0
х² + 20х - 300 = 0
Д = 400 + 1200 = 1600
х = (-20 + 400)/2 = 190
190 костюмов шила вторая мастерская в день.
ответ. 190