x₁ = 2 + 
, y₁ = 2 - 3;
x₂ = 2 -, y₂ = - 3 - 2:
Объяснение:
{ху - х = 4
{2х - у = 7
Выразим y и подставим во второе уравнение
{xy - x = 4
{-y = 7 - 2x
Уберём минус перед y, помножив выражение на (-1)
{xy - x = 4
{y = 2x - 7
Подставляем полученное выражение вместо y
x * (2x - 7) - x = 4
2x² - 7x - x =4
2x² - 8x - 4 = 0
Получаем квадратное уравнение. Сокращаем коэффиценты, деля обе стороны на 2
x² - 4x - 2 = 0
У нас a = 0. По теореме Виета: x₁ + x₂ = −b; x₁ * x₂ = c;
Но для начала проверим дискриминант
D = b² - 4ac
D = 16 - 4 * 1 * (-2)
D = 16 + 8 = 24
Нет такого натурального числа, которое было бы квадратным корнем из 24, поэтому мы не сможем решить теоремой Виета, и продолжаем решать дискриминантом
x₁,₂ = 
x₁ = 
= 
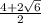= 2 +
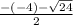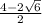x₂ = 
= 
= 2 -
Находим y, подставляя x
2 * (2 + ) - y₁ = 7
4 + 2 - y₁ = 7
- y₁ = 3 - 2
Убираем минус
y₁ = 2 - 3
Ищем y₂
2 * (2 - ) - y₂ = 7
4 - 2 - y₂ = 7
- y₂ = 3 + 2
Снова убираем минус
y₂ = - 3 - 2
ответ: x₁ = 2 + , y₁ = 2 - 3; x₂ = 2 -, y₂ = - 3 - 2;
Преобразуем 2 уравнение:
(x+y)^2-(x+y)=0
(x+y)(x+y-1)=0 - произведение равно 0, если хотя бы один множитель равен 0
в 1 уравнении делаем замену:
xy=t
получим:
t^2+2t=3
t^2+2t-3=0
D=4+12=16=4^2
t1=(-2+4)/2=1
t2=(-2-4)/2=-3
система разделится на 4 системы
1) xy=1
x+y=0
x=-y
-y^2=1
y^2=-1
y - нет решений
2) xy=1
x+y-1=0
x=1-y
(1-y)y=1
-y^2+y-1=0
y^2-y+1=0
D<0
y - нет корней
3) xy=-3
x+y=0
x=-y
-y^2=-3
y^2=3
y1=sqrt(3)
y2=-sqrt(3)
x1=-sqrt(3)
x2=sqrt(3)
4) xy=-3
x+y-1=0
x=1-y
(1-y)*y=-3
-y^2+y=-3
-y^2+y+3=0
y^2-y-3=0
D=1+12=13
y3=(1+sqrt(13))/2
y4=(1-sqrt(13))/2
x3=1-(1+sqrt(13))/2=(2-1-sqrt(13))/2=(1-sqrt(13))/2
x4=1-(1-sqrt(13))/2=(2-1+sqrt(13))/2=(1+sqrt(13))/2
ответ: (-sqrt(3);sqrt(3)), (sqrt(3);-sqrt(3)), ((1-sqrt(13))/2;(1+sqrt(13))/2), ((1+sqrt(13))/2;(1-sqrt(13))/2)
Объяснение:
вродебы так
Полученное выражение не зависит от a, т.е. оно равно двум при любом a,
в частности, и при a=0,17.
ответ: 2.