а) параллельна плоскости Oyz.
Уравнение плоскости, параллельной плоскости yOz, имеет вид: Ax + D = 0.
Подставляя в него координаты точки A, получим 3A + D = 0, или D = -3A.
Подставляя это значение в Ax + D = 0, получим
Ax - 3A = 0,
а сокращая на A, будем иметь окончательно
x - 3 = 0.
б) перпендикулярна оси Ox.
Так как плоскость перпендикулярна оси Ox, то она параллельна плоскости yOz, а потому ее уравнение имеет вид
Ax + D = 0.
Подставляя в это уравнение координаты точки A, получим, что D = -3A. Это значение D подставим вAx + D = 0 и, сокращая на A, будем иметь окончательно x - 3 = 0.
3,75 км/ч.
Объяснение:
Пусть скорость туриста на подъёме равна x км/ч, тогда его скорость на спуске равна ( x + 0,6 ) км/ч. Если спуск занял 1,5 часа, то пройденное за это время расстояние составит ( x + 0,6 ) * 1,5 = 1,5x + 0,9 км.
Если весь путь занял 2 часа, а спуск - 1,5 часа, то подъём занял 2 - 1,5 = 0,5 часа. За это время турист (двигаясь со скоростью x км/ч) 0,5 * x = 0,5x км.
Учитывая, что весь путь равен 7,2 км, можно составить уравнение:
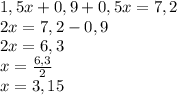
Скорость на подъёме составила 3,15 км/ч, следовательно скорость на спуске равна 3,15 + 0,6 = 3,75 км/ч.
a21=a1+20d=-0.5
отнимем от 1 ур-я 2
-15d=0,25
d=0,25: (-15)=1/4*(1/15)=-1/60
a1=a6-5d=-0,25-5*(-1/60)=-1/4+1/12=-3/12+1/12=-1/6
S26=(2a1+25d)*26/2=(2*(-1/6)+25*(-1/60)*13=(-1/3-5/12)*13=(-4/12-5/12)*13=
=-3/4*13=-39/4=-9 3/4=-9,75