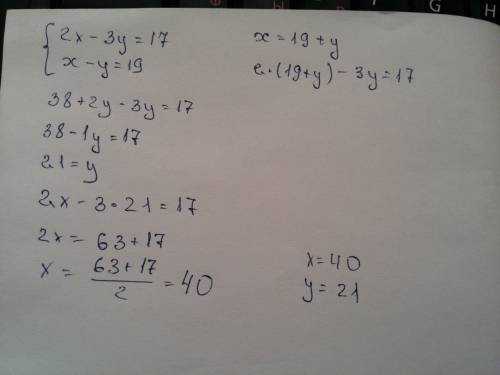
4
Запишем условие:
lgx + lg(x - 2) = lg(12 - x)
Складываем логарифмы в левой части, тогда:
lgx(x - 2) = lg(12 - x)
Так как 1 основание, решаем как обычное уравнение:
х(х - 2) = 12 - х
Раскороем скобки слева, откуда:
х^2 - 2х = 12 - х
Переносим правую часть влево, тогда:
х^2 - 2х - 12 + х = 0
Приводим подобные:
х^2 - х - 12 = 0
Решаем через дискриминант:
Находим дискриминант:
D = b^2 - 4ac
D = 1 - 4*1*(-12)
D = 1 - (-48)
D = 1 + 48 = 49
sqrt(D) = sqrt(49) = 7
x1 = (-b + sqrt(D))/2a = (1 + 7)/2 = 8/2 = 4
x2 = (-b - sqrt(D))/2a = (1 - 8)/2 = -3,5 - посторонний корень
Проверка:
Проверяем х1:
lg4 + lg(4 - 2) = lg(12 - 4)
lg4 + lg2 = lg8
Складываем логарифмы слева, тогда:
lg(4*2) = lg8
lg8 = lg8
Следовательно, х1 является действительным (правильным) корнем уравнения.
Проверяем х2:
lg(-3,5) + lg(-3,5 - 2) = lg(12 - 3,5)
lg(-3,5) + lg(-5,5) = lg8,5
Складываем логарифмы в левой части, тогда:
lg(19,25) > lg8,5
Следовательно, х2 посторонний корень данного уравнения.
ответ
Квадратное уравнение вида:
x^2 - 10x + 3 = 0
можно решить двумя
1) Как обычное квадратное уравнение типа
ax^2 + bx + c = 0 (тут a будет = 1)
Тогда решение будет по обычной формуле:
x(1,2) = [-b + -V{b^2 - 4*a*c}] / 2a = (при а=1) = [-b + -V{b^2 - 4c}] / 2
x(1) = [-b + V{b^2 - 4c}] / 2
x(2) = [-b - V{b^2 - 4c}] / 2
(здесь V - корень квадратный, и х(1) и х(2) отличаются знаком перед корнем)
Т.е уравнение x^2 - 10x + 3 = 0
x(1,2) = [10 + -V{10^2 - 4*3}] / 2 = [10 + -V88] /2 = 5 + -2V22
x(1) = 5 + 2V22
x(2) = 5 - 2V22
2) Второй решения - по теореме Виета:
x^2 + bx + c = 0
Сумма корней x1 и x2 будет равняться отрицательному значению коэффициента b.
x(1) + x(2) = - b
Произведение этих самых корней будет давать нам коэффициент c .
x(1) * x(2) = c
Т.е. уравнение x^2 - 10x + 3 = 0
x(1) + x(2) = -(-10) => x(1) + x(2) = 10 и
x(1) * x(2) = 3
Решив систему
{ x(1) + x(2) = 10
{ x(1) * x(2) = 3
найдешь корни уравнения.
Если уравнение неприведенное (коэффициент а не = 1) то теорема Виета будет:
{ x(1) + x(2) = - b/a
{ x(1) * x(2) = c/a