1. с) 4 см.
2. d) 14 см.
3. в) 8 см.
Объяснение:
". Основание равнобедренного треугольника равно 10 см., а боковая сторона 8 см. чему равна длина отрезка, соединяющего середины основания и боковой стороны?"
***
АВС - треугольник. АВ=ВС=8 см. MN - средняя линия треугольника MN║AB и равно его половине МН=АВ/2=8/2=4 см.
***
"В квадрате с диагональю 7 см последовательно соединили отрезками середины сторон. Найдите периметр образованного четырехугольника."
***
ABCD - квадрат. АС=7 см - диагональ квадрата.
Соединили середины сторон квадрата. Получили квадрат A1B1C1D1? стороны которого являются средними линиями диагоналей квадрата и равны его половине.
A1B1=B1C1=C1D1=A1D1=AC/2=7/2=3.5 см .
Р=4А1В1=4*3,5=14 см.
***
3. Средняя линия треугольника параллельна основанию и равна его половине.
АВС - равносторонний треугольник. MN =4 см - средняя линия. MN║AC. MN=AC/2. AC=2*MN=8 см .
Объяснение:
y=5ˣ.
Это показательная функция.
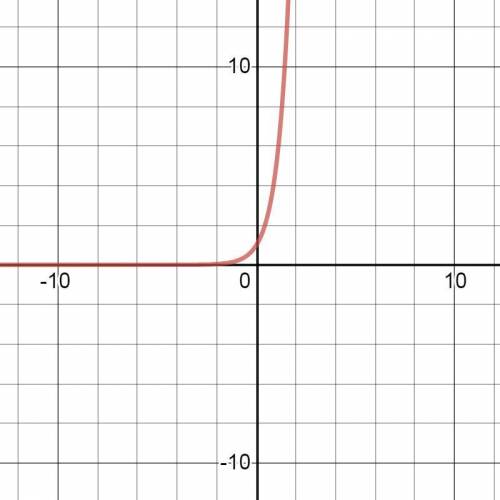
График этой функции показан на рис. 1.
Показательная функция y=5ˣ является строго монотонно возрастающей.
Область определения функции: х∈(-∞;+∞).
Область значений функции: у∈(0;+∞).
Точки пересечения с осью ОХ: нет.
Точки пересечения с осью ОУ: х=0 (0;1).
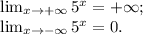
у=0,3ˣ
Это показательная функция.
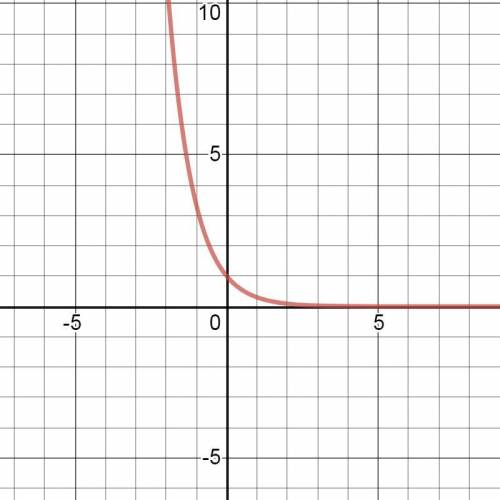
График этой функции показан на рис. 2.
Показательная функция у=0,3ˣ является строго монотонно убывающей.
Область определения функции: х∈(-∞;+∞).
Область значений функции: у∈(0;+∞).
Точки пересечения с осью ОХ: нет.
Точки пересечения с осью ОУ: х=0 (0;1).
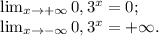
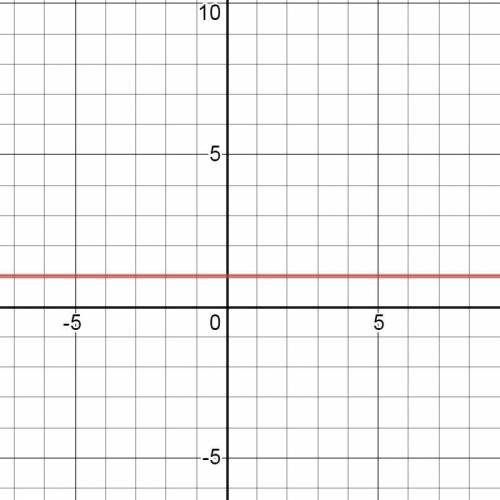
у=1ˣ.
График этой функции показан на рис. 3.
Единица в любой степени равена единице. ⇒
Получаем функцию у=1.
Графиком этой функции является график функции у=0 (ось ОХ),
смещённый вверх по оси ОУ на одну единицу.
Область определения функции: х∈(-∞;+∞).
Область значений функции: у=1.
Точки пересечения с осью ОХ: нет.
Точки пересечения с осью ОУ: х=0 (0;1).
2)3,5-17,5=-14
3) (3/14)*(-14)= -3.
ответ: -3.