Иррациона́льное число́ — это вещественное число, которое не является рациональным, то есть не может быть представлено в виде обыкновенной дроби {\displaystyle \pm {\frac {m}{n}}}{\displaystyle \pm {\frac {m}{n}}}, где {\displaystyle m,n}m,n — натуральные числа. Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.
Иррациональные числа
ζ(3) — ρ — √2 — √3 — √5 — ln 2 — φ,Φ — ψ — α,δ — e — {\displaystyle e^{\pi }}e^{\pi } и π
Другими словами, множество иррациональных чисел есть разность {\displaystyle \mathbb {I} =\mathbb {R} \backslash \mathbb {Q} }{\displaystyle \mathbb {I} =\mathbb {R} \backslash \mathbb {Q} } множеств вещественных и рациональных чисел.
О существовании иррациональных чисел (точнее отрезков, несоизмеримых с отрезком единичной длины), знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа {\displaystyle {\sqrt {2}}}{\sqrt {2}}[1].
К числу иррациональных чисел относятся отношение π окружности круга к его диаметру, число Эйлера e, золотое сечение φ и квадратный корень из двух[2][3][4]; на самом деле все квадратные корни натуральных чисел, кроме полных квадратов, иррациональны.
Иррациональные числа также могут рассматриваться через бесконечные непрерывные дроби. Следствием доказательства Кантора является то, что действительные числа неисчислимы, а рациональные счетны, отсюда следует, что почти все действительные числа иррациональны[5].
и 
. Чтобы найти для них общий знаменатель, нужно найти найменьшее общее число которое нацело делилось бы на знаменатель первого и второго дроба, в даном случае знаменатели это 25 и 4. Ну можно взять больший знаменатель умножить на 2 и проверить делится ли это число нацело на первый и другой знаменатель, если не делится ужножаеш на 3 и проверяеш, и так далее. Часто бывает, что один с знаменателей уже делится на себя и на второй знаменатель, тогда это и будет общий знаменатель. Потом оно само будет получаться, потому что будешь знать что на что делится.+ ;
;
= 
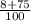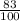, если можно сократить (то есть и числитель и множитель делится на одинаковое число), то сокращаем.
2cos^2x=-cosx
2cos^2x-cosx=0
cosx(2cosx-1)=0
cosx=0
x=+-п/2+2пn
2cosx+1=0
2cosx=-1
cosx=1/2
x=+-п/3+2пn