Сегодня был хороший денёк. Я не знаю, что на меня нашло, но мне хотелось пойти в церковь. Так я и сделал. Прийдя, я рассматривал иконостасы и иконы, слушал исповеди и прочее. Потом, батюшка подошёл ко мне и сказал: " Я вижу ты ороший мальчик, пойдём я тебе что-то расскажу!". Удалясь из залы, он повёл меня в какую-то комнату. Затем, он угостил меня чаем и пирогом. Сначала я его не слушал, поскольку был занят поеданием пирога, а потом я начал слушать батюшку. Он мне рассказывал про какого-то Моисея, который спустившись с горы Арарат, где долго молился Богу, принёс каменную дощечку на которой были написаны 10 заповедей.
(Перечислишь сам их, окей?)
Послушав их, я долго думал над значением, посколько батюшка, сказл: " Ты сам должен понять смысл, мой юный друг!"
Я постоянно думал про эти заповеди. Зачем их дал Бог? Почему именно эти? Почему именно 10, а не 12 или 20?
Повзрослев, я стал понимать. Но на выполнение этих 10 заповедей, мне так и не хватало силы воли, но относится к христианству я стал иначе.
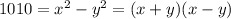
1010 - чётное число, чтобы разность была чётная, то оба квадрата должны одновременно быть либо чётными, либо нечётными, т.е. эти натуральные числа или оба чётные, или оба нечётные.
Разложим 1010 на простые множители: 1010=2*5*101
Число 1010 можно представить в виде произведения двух сомножителей:
1010=1010*1
1010=505*2
1010=202*5
1010=101*10
В любом случае получается, что один из сомножителей чётный, а другой нечётный. В случае же если оба числа чётные или оба нечётные, то сумма и разность этих двух чисел могут быть только чётными числами. Поэтому число 1010 нельзя представить в виде разности квадратов двух натуральных чисел.
ответ: НЕТ.
b₂=-6,9
Найдем разность арифм. прогрессии
d=b₂-b₁
d=-6.9-(-7.2)
d=0.3
найдём число отрицательных членов данной прогрессии с формулы n члена арифм. прогрессии:
а (n) = b₁ +d(n-1)
т.к нужно найти отрицательные члены(<0), то переделываем данную формулу в неравенство:
b₁ +d(n-1)<0
-7.2+0.3(n-1)<0
-7.2+0.3n+0.3<0
-6.9+0.3n<0
0.3n<6.9
n<6.9/0.3
n<23
Значит, последний отрицательный член арифм.прогрессии #22.
Находим сумму всех отрицательных членов арифметической прогрессии:
S=((2а₁+(n-1)*d) /2)*n
S=((2*(-7.2)+(22-1)*0.3) /2)*22- сокращаем 2 и 22
S=(2*(-7.2)+(22-1)*0.3)*11
S=(-14.4+21*0.3) *11
S=(-14.4+6.3) *11
S=(-8.1)*11
S=-89.1