0
Объяснение:
Находим точку, симметричную точке (2;-3) относительно оси ординат. Для этого надо поменять знак у абсциссы. Получаем точку (-2;-3)
Находим общее уравнение прямой, параллельной y = 1,5x -2,5.
у = 1,5х -2,5 => k=1,5 => y = 1,5x +b
Находим b. Для этого в уравнение y = 1,5x +b подставляем координаты точки принадлежащей данной прямой, т.е. точки (-2;-3)
1,5*(-2)+b = -3
-3+b = -3
b = -3+3
b = 0
Итак, y =1,5x - уравнение параллельной прямой у=1,5х-2,5 и проходящей через точку, симметричную точке (2;-3) относительно оси ординат.
Теперь находим абсциссу точки пересечения найденной прямой с осью абсцисс.
у = 0 - уравнение оси абсцисс
1,5 х = 0
х = 0:1,5
х = 0
(0;0) - точка пересечения прямой у=1,5х с осью Ох
х = 0 - искомая абсцисса
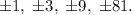
lg(x)=0
x=10^0=1
lg^2(x)-lg(x)-6=0
lg(x)=a
a^2-a-6=0
корни -2 и 3
то lg(x)=-2; x=10^(-2); x=0.01
lg(x)=3; x=10^2=1000;
log(по основанию )(3^x - 6) = x-1
3^(x-1)=3^x-6
3^x=3*3^x+6
3^x-3*3^x=-6
-2*3^x=-6
3^x=3
x=1
log(по основанию 3)(4*3^x -1) = 2x+1
3^(2x+1)=4*3^x-1
3*3^2x-4*3^x+1=0
3^x=a
3a^2-4a+1=0
корни 1 и 3
3^x=1 => x=0
3^x=3 => x=1