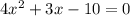, если их несколько, то указать сумму. 
): 
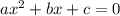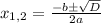, дискриминант же расписывается по-своему: 
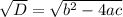. Дискриминант как бы заслужил своё отдельное внимание, ведь именно при его вычислении люди нередко допускают ошибки. Теперь – решаем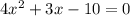, отсюда: 
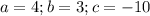, значит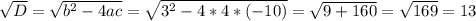
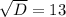; это как в алгебраических выражений седьмого класса – ты складываешь буквы, подставляешь вместо них какие-то числа и считываешь ответ, так вот здесь тоже самое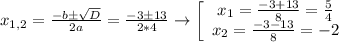
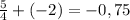
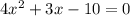равна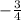 
x²+x²-2x+4-4=0
2x²-2x=0
2x(x-1)=0
x1=0
x2=1
Мы нашли пределы интегрирования, теперь берем определенный интеграл от 0 до 1 от функции
x²- 2x³/3 подставляем наши пределы 1²-(2*1³/3)-(0²-2*0³/3)= 1-2/3= 1/3
Площадь фигуры равна 1/3! Нарисуй графики и убедишься что площадь меньше одной клеточки.