10/25-x^2 - 1/5+x - x/x-5 = 0
По формулам сокращенного умножения (а^2 - в^2) = (а + в)(а - в)
10/(5-х)(5+х) - 1/(5+x) + x/(5-х) = 0 (здесь поменяли знак на +, и дробь изменилась)
Общий знаменатель (5-х)(5+х)
Получаем в числителе Знаменатель
10-5+х+5х+х^2 = 0 (5-х)(5+х) не равно 0
х^2+6х+5 = 0 5-х не равно 0, х не равен 5
Д = 36-4*1*5 = 36-20 = 16 5+х не равно 0, х не равен -5
х1 = (-6+4) / 2 = -1
х2 = (-6-4) / 2 = -5 не берем
ответ: х = -1
a) 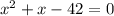
Ищем дискриминант:
D=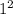 -4*1*(-42)=1-4*(-42)=1-(-4*42)=1-(-168)=1+168=169;
-4*1*(-42)=1-4*(-42)=1-(-4*42)=1-(-168)=1+168=169;
Дискриминант больше 0, уравнение имеет 2 корня: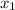 =
=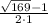 =(13-1)/2=12/2=6;
=(13-1)/2=12/2=6;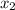 =
= 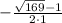 =(13-1)/2=12/2=6 =(-13-1)/2=-14/2=-7.
=(13-1)/2=12/2=6 =(-13-1)/2=-14/2=-7.
б) 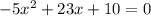
Ищем дискриминант:
D=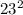 -4*(-5)*10=529-4*(-5)*10=529-(-4*5)*10=529-(-20)*10=529-(-20*10)=529-(-200)=529+200=729;
-4*(-5)*10=529-4*(-5)*10=529-(-4*5)*10=529-(-20)*10=529-(-20*10)=529-(-200)=529+200=729;
Дискриминант больше 0, уравнение имеет 2 корня: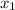 =
= 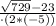 =(27-23)/(2*(-5))=4/(2*(-5))=4/(-2*5)=4/(-10)=-4/10=-0.4;
=(27-23)/(2*(-5))=4/(2*(-5))=4/(-2*5)=4/(-10)=-4/10=-0.4;
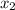 =
= 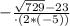 =-50/(2*(-5))=-50/(-2*5)=-50/(-10)=-(-50/10)=-(-5)=5.
=-50/(2*(-5))=-50/(-2*5)=-50/(-10)=-(-50/10)=-(-5)=5.
в) 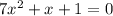
Ищем дискриминант:
D=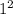 -4*7*1=1-4*7=1-28=-27;
-4*7*1=1-4*7=1-28=-27;
Дискриминант меньше 0, уравнение не имеет корней.
г) 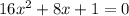
Ищем дискриминант:
D= 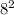 -4*16*1=64-4*16=64-64=0;
-4*16*1=64-4*16=64-64=0;
Дискриминант равен 0, уравнение имеет 1 корень:
X=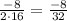 =-0.25
=-0.25
Графиком квадратичной функции является парабола, что вершину в начале координат и проходит через точку А (2; -8). Задайте эту функцию формулой
Решение:
Уравнение параболы задается уравнением
y =ax²+bx+с или х = ay²+by+с(данное уравнение можете не рассматривать)
где а≠0
Так как вершина параболы находится в начале координат то b=c=0
Уравнение параболы можно записать как:
y =ax² или х = ay²(данное уравнение можете не рассматривать)
Найдем постоянную величину а из уравнений подставив координаты точки А(2;-8)
а = у/х² = -8/2² =-8/4=-2
y = -2x²
a = x/y² =2/(-8)² =2/64 =1/32
x = y²/32 (данное уравнение можете не рассматривать)
Рішення :
Рівняння параболи задається рівнянням
y = ax ² + bx + з або х = ay ² + by + з
де а ≠ 0
Так як вершина параболи знаходиться на початку координат то b = c = 0
рівняння можна записати як
y = ax ² або х = ay ²
Знайдемо постійну величину а з рівнянь підставивши координати точки А (2; -8)
а = у / х ² = -8 / 2 ² = -8/4 = -2
y =-2x ²
a = x / y ² = 2 / (-8) ² = 2/64 = 1/32
x = y ² / 32