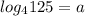
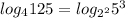 .
. 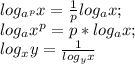 .
. 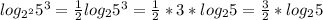
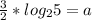 , тогда, следовательно,
, тогда, следовательно, 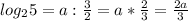 .
. 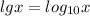 . На примере, думаю, всё наглядно понятно. Едем.
. На примере, думаю, всё наглядно понятно. Едем. 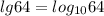 . Шестьдесят четыре – это два в шестой степени, посему имеем право записать:
. Шестьдесят четыре – это два в шестой степени, посему имеем право записать: 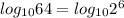 . Но и не забываем про свойства, описанные немного ранее:
. Но и не забываем про свойства, описанные немного ранее: 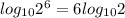 .
.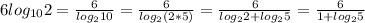 .
. 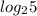 ... кажется, где-то он есть в решении, да причём и равен
... кажется, где-то он есть в решении, да причём и равен 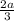 ! Подставляем в слагаемое, находящееся в знаменателе дроби, сокращаем, перемножаем, складываем – считаем, короче.
! Подставляем в слагаемое, находящееся в знаменателе дроби, сокращаем, перемножаем, складываем – считаем, короче. 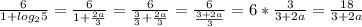
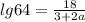 , если
, если 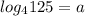 .
.
Пусть во втором ящике x гвоздей, тогда в первом ящике 2x гвоздей. После того, как взяли 5кг из первого, там осталось 2x-5. А после того, как взяли 10кг из второго, там осталось x-10
По условию 2x-5=3*(x-10)
Решаем уравнение:
2x-5=3x-30
3x-2x=30-5
x=25
Значит, во втором ящике первоначально было 25кг гвоздей, а во втором - 50кг гвоздей. Всего в этих ящиках было 50+25=75кг гвоздей
ответ: в двух ящиках первоначально было 75кг гвоздей.