Відстань між пунктами а і в рівна 96 км. із пункту а вниз за течією відправили пліт. одночасно з цим із пункту в назустріч із плотом відплив моторний човен і зустрівся з ним через 4 год. яка власна швидкість (км/год) човна, якщо швидкість течії річки рівна 3 км/год?

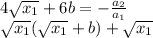
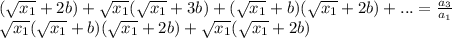
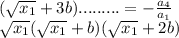
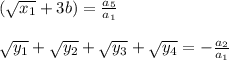
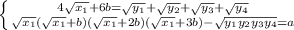
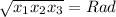 , то произведение корней так же число радикальное , откуда с последних двух идет верное равенство
, то произведение корней так же число радикальное , откуда с последних двух идет верное равенство
у - скорость катера относительно воды
S = x*t + (y-x)*t = y*t
y=S/t = 96 км/4 час = 24 км/час