х€(0; +оо)
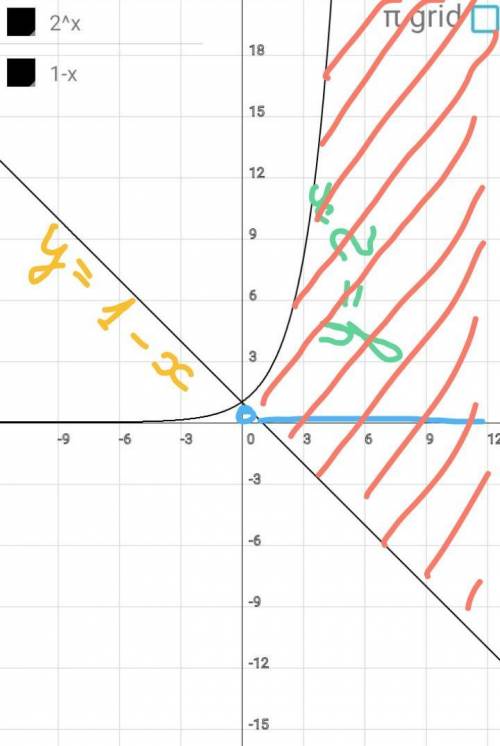
Графическое решение
неравенств.
Объяснение:
Шаг 1.
Строим график функции
у=2^х.
Показательная функция
а>1 ==> функция возрастает.
Пересекает ось ординат в
точке х=0.
у(0)=2^0=1
Шаг 2.
Строим график фцнкции
у=1-х или у=-х+1.
Линейная функция k<0
==> функция убывает.
Пересекает ось ординат в
точке х=0.
у(0)=0+1=1
Шаг 3.
В одной системе координат
строим графики функций
(по точкам).
Графики пересекаются в
точке (0; 1).
Шаг4.
Графически решаем задан
ное неравенство:
определяем участки, на кото
рых график функции у=2^х
расположен выше графика
функции у=-х+1.
х€(0; +оо).
х€(0; +оо)
1)2cosx+1=0, cosx=-1/2, x=+-2π/3+2πk, k∈z
2sinx-√3=0, sinx=√3/2, x=(-1)^k*π/3+kπ,k∈z
2) cosx(2-3sinx)=0,sinx=0,x=πk,k∈z
2-3sinx=0, sinx=2/3, x=(-1)^k arcsin2/3+πk,
3)sinx(4sinx-3)=0, sinx=0, x=πk,k∈z
4sinx-3=0 sinx=3/4, x=(-1)^karcsin3/4+πk,k∈z
4)(sin^2(x)=1/2,x=+-π/4+πk,k∈z.
5)6sin^2(x)+sinx-2=0,Sinx=t, 6t^2+t-2=0 , его корни t1=-2/3,t2=1/2,
sinx=-2/3,x=(-1)^(k+1)arcsin2/3+πk,k∈z, sinx=1/2,x=(-1)^kπ/6+πk,k∈z.
6) 3cos^2(x)-7sinx-7=0,Заменим косинус на синус получим
3sin^2(x)+7sinx+4=0, его корни sinx=-8/6- корней нет, sinx=-1, x= -π/2+2πk,k∈z
Объяснение:
Пусть Х - скорость первого
х - 8 - скорость второго
500 - 272 = 228 км - проехали за 1,5 часа
1,5 * (х + х - 8) = 228
1,5х + 1,5х - 12 = 228
3х = 228 + 12
3х = 240
х = 240 : 3
х = 80 км/ч - скорость первого
80 - 8 = 72 км/ч - скорость второго
проверим:
1,5 * 80 = 120 км - проехал первый
1,5 * 72 = 108 км - проехал второй
120 + 108 = 228 км - проехали вместе
500 - 228 = 272 км - оставшееся расстояние.
2
Х - скорость первого
х + 6 - скорость второго
30 мин = 0,5 ч
120 - 79 = 41 км - проехали за 0,5 часа
0,5 * (х + х + 6) = 41
0,5х + 0,5х + 3 = 41
х = 41 - 3
х = 38 км/ч - скорость первого
38 + 6 = 44 км/ч - скорость второго
Проверим:
0,5 * 38 = 19 км - проехал первый
0,5 * 44 = 22 км - проехал второй
19 + 22 = 41 км - проехали всего
120 - 41 = 79 км - оставшееся расстояние