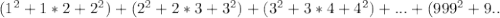
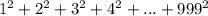 по известной формуле
по известной формуле 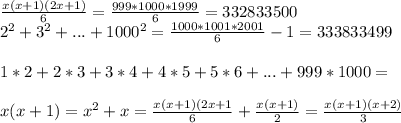
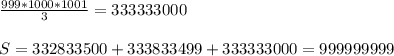
вам нужны формулы "косинус двойного угла" и "косинус суммы углов"
cos2x=2cos^2x-1
cos(x+y)= cosx*cosy-sinx*siny
отсюда, преобразовуя ваш пример/ имеем
5cos2x+7(cosx*cosП/2-sinx*sinП/2)+1=0
cosП/2=0 sinП/2=1, значит
5cos2x+7(-sinx)+1=0
10cos^2x-1-7sinx+1=0
10cos^2x=7sinx
10-10sin^2x=7sinx
10sin^2x+7sinx-10=0, а дальше ищем дискриминант, ибо это квадратное уравнение.
Фух! забодался я. Молодой человек, сборник Сканави (как я сразу не просек) не для того придумали, чтобы вы ответы в сети искали. Лучше попробуйте сами порешать. Если хотя бы 20% одолеете, вам все местные задачки будут по плечу.
1) Это формула квадрата суммы: (x+3)^2>=0, здесь х - любое число, так как квадрат любого выражения всегда неотрицательное число. ответ: (-беск; +беск)
2) Приводим подобные: 1,5х-4<0. 1,5x<4, делим на 1,5=3/2: x<(4*2)/3, x<8/3,
x<2целых 2/3, т.е. ответ (-беск; 2целых2/3)
3) 2x^2<=x, 2x^2 -x<=0, x(2x-1)<=0. Метод интервалов. x(2x-1)=0, отсюда
х=0 или 1/2/ Наносим на числовую прямую найденные числа и расставляем знаки. Получим: на промежутке (-беск; 0] знак "-" , на промежутке [0; 1/2] знак "+" б
на промежутке [1/2; +беск) знак "-". Нам нужен промежуток с минусом. Это
[0; 1/2]