Question

Найдите наибольшее целочисленное решение неравенства f(x)-f ' (x)< 0, если f(x)=3x^2+18x+8.

Answer 1

f(x) = 3x²+18x+8;

f'(x) = 2·3x+18·1+0 = 6x+18.

f(x) - f'(x) < 0;

3x²+18x+8 - (6x+18) < 0;

3x²+18x-6x+8-18 < 0;

3x²+12x-10 < 0 (1)

Найдём х, при которых выражение равно нулю:

D = 12²-4·3·(-10) = 144+120 = 4·66

x =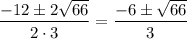 $\dfrac{-12\pm 2\sqrt{66}}{2\cdot 3} =\dfrac{-6\pm \sqrt{66}}{3}$

Решим неравенство (1) методом интервалом, смотри в приложении.

$\dfrac{-6-\sqrt{66}}3$

Необходимо найти наибольшее целое число, которое меньше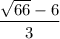 $\dfrac{\sqrt{66}-6}3$

$\sqrt{64}$

ответ: 0.