2. б), г); 3.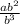 
.
Объяснение:
Задание №2.
Большинство выражений в вариантах ответа представлены алгебраическими дробями.
Дробь не имеет смысла, если её знаменатель равен нулю, так как по правилу на ноль делить нельзя.
Подставим в каждый вариант ответа значение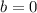 
и вычислим полученное выражение.
а) 
Выражение имеет смысл, поэтому этот вариант нам не подходит.
б)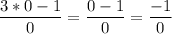 
Выражение не имеет смысл, т.к. знаменатель равен нулю, поэтому этот вариант нам подходит.
в)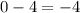 
Выражение имеет смысл, поэтому этот вариант нам не подходит.
г)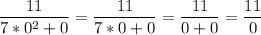 
Выражение не имеет смысл, т.к. знаменатель равен нулю, поэтому этот вариант нам подходит.
Задание №3.
Для того, чтобы привести дробь к определённому знаменателю, нужно знаменатель этой дроби (числитель по правилу соответственно) домножить на такое число, чтобы произведение было равно искомому знаменателю.
В данном случае нужно домножить дробь на 
.
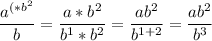
Эта дробь и будет являться ответом данного задания.
Объяснение:
1) n^3 - n = n(n^2 - 1) = n(n-1)(n+1)
Это произведение трех последовательных чисел.
Хотя бы одно из этих чисел четное. Если какое-то из чисел делится на 5, то произведение делится на 10.
2) Пусть ни одно из чисел n-1, n, n+1 не делится на 5. Тогда n при делении на 5 может давать остаток 2 или 3, то есть n = 5k+2 или n = 5k+3.
Разложим n^3 + n = n(n^2 + 1)
Найдем n^2 + 1 для обоих этих случаев.
a) n = 5k + 2
n^2 + 1 = (5k+2)^2 + 1 = 25k^2 + 20k + 4 + 1 = 25k^2 + 20k + 5
b) n = 5k + 3
n^2 + 1 = (5k+3)^2 + 1 = 25k^2 + 30k + 9 + 1 = 25k^2 + 30k + 10
В обоих случаях число n^2 + 1 делится на 5.
При этом заметим, что если n четное, то произведение n(n^2 + 1) делится на 10, а если n нечетное, то n^2 + 1 четное, и при этом оно же делится на 5, то есть оно делится на 10.
3) Таким образом, мы доказали, что либо n^3 - n = n(n-1)(n+1),
либо n^3 + n = n(n^2 + 1) делится на 10.
3х+1=0
3х=-1
х=-1/3