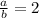
Числа 4 и 5 - корни уравнения, тогда имеем
2·4² + b·4 + с = 0
и
2·5² + b·5 + c = 0
Решаем эту систему из двух уравнений на два неизвестных.
32 + 4b + c = 0,(*)
50 + 5b + c = 0,
Из последнего уравнения вычтем предпоследнее уравнение:
50 + 5b + c - (32 + 4b + c) = 0 - 0,
50 - 32 + 5b - 4b + c - c = 0,
18 + b = 0,
b = -18,
подставим найденное значние, например, в (*), имеем
32 + 4·(-18) + с = 0,
32 - 72 + с = 0,
-40 + c = 0,
c = 40.
Тогда исходное уравнение имеет вид
2·x² - 18·x + 40 = 0,
D = (-18)² - 4·2·40 = 324 - 320 = 4 < 5.
Итак, дискриминант меньше 5.
ответ. Неверно.
С этого метода постановки практически всегда можно решить систему уравнений.
Алгоритм решения системы двух уравнений с двумя переменными методом подстановки:
1. из любого (обычно более уравнения системы выразить одно неизвестное через другое,
например, x через y из первого уравнения системы;
(Чтобы выразить неизвестное, нужно выполнить два условия:
1-перенести неизвестное, которое хотим выразить, в левую часть уравнения;
2- разделить и левую и правую часть уравнения на нужное число так, чтобы коэффициент при неизвестном стал равным единице. )
2. подставить полученное выражение в другое (второе) уравнение системы вместо x;
3. решить уравнение с одним неизвестным относительно y (найти y);
4. подставить найденное на третьем шаге значение y в уравнение,
полученное на первом шаге, вместо y и найти x;
5. записать ответ мой ответ в лучшие)))
б. х*у=9
в. b = с
г. 2p = 3 g