Объяснение:
1) ОДЗ: 2x+1>0, x>-1/2 u 3x-7>0, x>7/3, основания равны, 2x+1=3x-7, x=8
2) ОДЗ: x>0 u x+2>0, x>-2, значит, x>0,
log2 (x*(x+2))=3, x^2+2x=2^3, x^2+2x-8=0, корни х=2 и х=-4(не
удовлетворяет ОДЗ), отв. х=2
3)обозначим lgx=t/ x>0, t^2-3t+2=0, t=1 u t=2, тогда, lgx=1, x=10,
lgx=2, x=10^2=100, отв: 10 и 100 (^ -знак степени)
1) ОДЗ: 4x+3>0, x>-3/4, т.к. основание >1, то 4x+3>16^ 1/2,
4x+3>4, 4x> 1, x> 1/4
2) ОДЗ: х>0, пусть t=log4 x, тогда, t^2-2t-3<0, , корни t=3 u t=-1,
-1<t<3, -1<log4 x<3, 1/4<x<4^3, 1/4<x<64
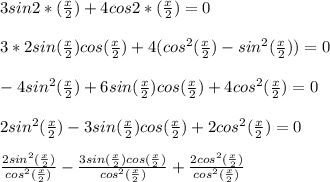 =0
=0
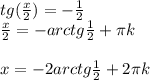 ,
,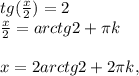
 k∈Z;
k∈Z;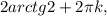 k∈Z.
k∈Z.
вроде так. если нет-то прости)