tg2x-sec2x
Объяснение:
умножим числитель и знаменатель первой дроби на sinx-cosx
тогда числитель (sinx-cosx)²,знаменатель sinx²-cosx²
Раскроем числитель по ФСУ тогда sinx²+cosx²-2sinxcosx, а в знаменателе вынесем -1, тогда cosx²-sinx² по ОТТ и формуле двойного угла для синуса числитель равен 1-sin2x, а знаменатель по формуле двойного угла для косинуса равен -cos2x. Почленно поделим на -cos2x, тогда получим tg2x-1/cos2x, по определению, величина обратная косинусу есть секанс, окончательно получаем tg2x-sec2x
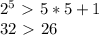 .
. 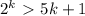 .
.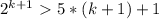
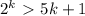 =>
=> 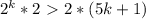 =>
=> 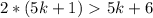
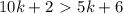 .
. 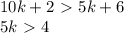
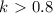 .
.
5 и -10 -целые и кратные 5
100 и 500002 - целые и положительные (натуральные)
53 и 59 -- простые и больше 50