
v₁ = 3км/час, v₂ = 5км/час
Объяснение:
1час15 мин = 75мин
1час = 60 мин
v₁ - скорость 1-ого пешехода
v₂ - скорость 2-ого
1) 1-е уравнение:
75(v₁ + v₂) = 10
2)
Т.к 1-ый пешеход вышел на 40мин раньше, то, если до встречи 2-ой пешеход шёл 1час = 60мин., то первый на 40мин. больше:
40мин + 60мин= 100мин. Получаем 2-е уравнение:
100v₁ + 60₂ = 10
3) Решаем систему (методом сложения):
{ 75v₁ + 75v₂ = 10 | * (-2)
{100v₁ + 60v₂ = 10 | * 2,5
{ -150v₁ - 150v₂ = 20
{ 250v₁ + 150v₂ = 25
100v₁ = 5
v₁ = 5/100 = 0,05 (км/мин) = 3км/час - скорость 1-ого пешехода.
Из 2-ого уравнения находим v₂ (км/мин), подставляя в него значение
v₁ =0,05км/мин:
100v₁ + 60v₂ = 10 → 60v₂ = 10 - 100*0,05 → 60v₂ = 5
v₂ = 5/60 = 1/12 (км/мин) = 5 км/час - скорость 2-ого пешехода
Для начала найдём, сколько слабо успевающих учеников.
1) 25-(10+3) = 12 - слабо успевающие
Наше событие(А) - это "не ниже 4", значит, оценка 4 или 5
Обозначим вероятности (P) того, что вызванный ученик окажется или отличником(У1), или ударником(У2), или слабо успевающим(У3).
P(У1) = 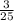
Р(У2) = 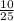
Р(У3) = 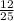
Вероятность того, что У1 ответит на оценку, не ниже 4 = 100%
Вероятность того, что У2 ответит на оценку, не ниже 4 = 100%, так как на экзамене он с равной долей вероятности получит или 4, или 5
Найдём Вероятность того, что У3 ответит на экзамене не ниже 4. С равной долей вероятности он может получить 3(О1) или 4(О2) или 5(О3). Вероятность получить одну из данных отметок равна 1/3.
P(O1)=P(O2)=P(O3)= 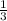
Благоприятному исходу соответствуют 2 случая: 4 или 5. Значит, вероятность получения одной из двух этих отметок равна
P(O2+O3)=P(O2)+P(O3)= 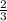
Вероятность события (А) =
P(A)=P(У1)*1+Р(У2)*1+P(У3)*P(O2+O3)= 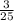 +
+ 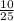 +
+ 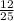 *
*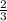 =
=
0,12+0,4+0,32= 0,48
ответ: 0,48