а=4, в=25, с=29, д=13
S=((а+в)/2)* sqrt{с^2-((в-а)^2+с^2-д^2)/2(в-а))^2}
S=((a+в)/2*sqrt{20^2-((21^2+20^2-13^2)/2*21)^2}
S=((а+в)/2*sqrt{400-((441+400-169)/42)^2}=
=((а+в)/2)*sqrt{400- 256}=((а+в)/2)*sqrt{144}
отсюда h=sqrt{144}=12
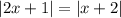
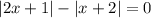
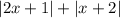
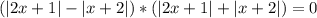
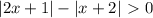
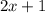 и
и 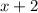 принимают значение
принимают значение 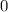 при различных значениях
при различных значениях  , по этому сумма указанных выше двух модулей всегда строго положительна)
, по этому сумма указанных выше двух модулей всегда строго положительна)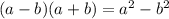 :
: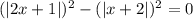
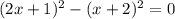
![[(2x+1)-(x+2)]*[(2x+1)+(x+2)]=0](/tpl/images/0599/8070/031a8.png)
![[x-1]*[3x+3]=0](/tpl/images/0599/8070/f7400.png)
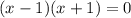
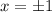
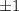


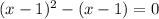

![(x-1)*[(x-1)-(1)]=0](/tpl/images/0599/8070/f134d.png)
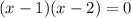
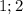
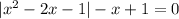
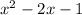
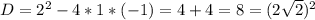
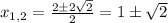
![|[x-(1- \sqrt{2} )]*[x-(1+ \sqrt{2} )]|-x+1=0](/tpl/images/0599/8070/ef287.png)
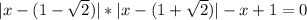
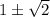 разбивают множество действительных чисел на три интервала:
разбивают множество действительных чисел на три интервала:![x\in(-\infty;1- \sqrt{2}]](/tpl/images/0599/8070/b7e08.png) , то имеем уравнение (оба модуля раскрываются с минусом):
, то имеем уравнение (оба модуля раскрываются с минусом):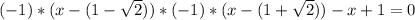
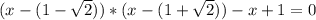
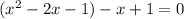
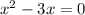
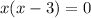
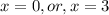
![(-\infty;1- \sqrt{2}]](/tpl/images/0599/8070/ee814.png) , значит из этой ветки корней для исходного уравнения не оказалось
, значит из этой ветки корней для исходного уравнения не оказалось![x\in(1- \sqrt{2};1+ \sqrt{2} ]](/tpl/images/0599/8070/340ea.png) (один модуль раскрывается с минусом, а второй с плюсом), то:
(один модуль раскрывается с минусом, а второй с плюсом), то: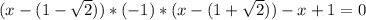
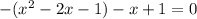
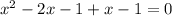
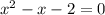
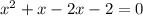
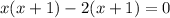
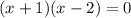
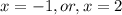
![(1- \sqrt{2};1+ \sqrt{2} ]](/tpl/images/0599/8070/a7e75.png) попадает лишь корень
попадает лишь корень 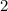 - первое найденное решение исходного уравнения
- первое найденное решение исходного уравнения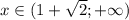 то оба модуля раскрываются с плюсом, и мы получаем точно такое же уравнение, как и в случае 1)
то оба модуля раскрываются с плюсом, и мы получаем точно такое же уравнение, как и в случае 1)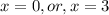 . В указанный интервал попадает лишь корень
. В указанный интервал попадает лишь корень 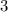 - второе и последнее решение исходного уравнения.
- второе и последнее решение исходного уравнения.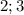
Числовые, буквенные выражения и выражения с переменными бывают составлены с использованием скобок, которые могут указывать порядок выполнения действий, содержать отрицательное число и т.п. Бывает удобно перейти от этого выражения со скобками к тождественно равному выражению, которое уже не содержит этих скобок. К примеру, от выражения 2·(3+4) можно перейти к выражению без скобок вида2·3+2·4. Этот переход от выражения со скобками к тождественно равному выражению без скобок дает представление о раскрытии скобок.
В школьном курсе математики к раскрытию скобок подходят в 6 классе. На этом этапе под раскрытием скобок понимают избавление от скобок, указывающих порядок выполнения действий. А изучают раскрытие скобок при рассмотрении выражений, которые содержат:
знаки плюс или минус перед скобками, заключающими суммы и/или разности, например, (a+7) и −(−3+2·a−12−b);произведение числа, одной или нескольких букв и суммы и/или разности в скобках, например, 3·(2−7), (3−a+8·c)·(−b) или −2·a·(b+2·c−3·m).Однако ничто не мешает раскрытие скобок рассматривать немного шире. Почему бы не назвать раскрытием скобок переход от выражения, содержащего отрицательные числа в скобках, к выражению без скобок, например, переход от 5+(−3)−(−7) к5−3+7? Или замена произведения выражений в скобках вида (a+b)·(c+d) на суммуa·c+a·d+b·c+b·d противоречит смыслу раскрытия скобок?
Можно пойти еще дальше. Допустим, что в описанных выше выражениях вместо чисел и переменных могут быть любые выражения. В полученных таким выражениях тоже можно проводить раскрытие скобок. Для иллюстрации возьмем выражение , ему соответствует выражение без скобок вида .
Итак, мы под раскрытием скобок будем понимать избавление от скобок, указывающих порядок выполнения действий, а также избавление от скобок, в которые заключены отдельные числа и выражения.
И обратим внимание еще на один момент, касающийся особенностей записи решения при раскрытии скобок. Начальное выражение со скобками и результат, полученный после раскрытия скобок, удобно записывать в виде равенства. Например, выражение3−(5−7) после раскрытия скобок принимает вид 3−5+7, это наглядно отражает равенство 3−(5−7)=3−5+7. При раскрытии скобок в громоздких выражениях возникает необходимость в записи промежуточных результатов, в этом случае решение удобно оформлять в виде цепочки равенств, к примеру,5−(3−(2−1))=5−(3−2+1)=5−3+2−1 или 5−(3−(2−1))=5−3+(2−1)=5−3+2−1.
AB = 29, BC = 4, CD = 13, AD = 29, Проведем две высоты: ВМ и СК. (=h).
Из пр. тр-ов АВМ и СDK по т. Пифагора найдем отрезки АМ и КD:
АМ = кор( АВ^2 - h^2) = кор(841 - h^2)
KD = кор(CD^2 - h^2) = кор(169 - h^2)
Из рисунка легко увидеть: АМ + KD = 25 - 4 = 21
Получим уравнение:
кор(841-h^2) = 21 - кор(169-h^2)
841-h^2 = 441 - 42кор(169 -h^2) + 169 - h^2
42кор(169 - h^2) = - 231 - это невозможно. Значит чертеж надо делать другой!
Боковые стороны обе наклонены в одну сторону.
Высота СК будет опущена на продолжение стороны AD. и :
AD + DK - BC = AM
21+кор(169-h^2)= кор(841 - h^2)
841-h^2 = 441 + 42кор(169 -h^2) + 169 - h^2
42кор(169 - h^2) = 231
кор(169 - h^2) = 11/2
169 - h^2 = 121/4
h^2 = 169 - 21/4 = 655/4
h = (кор655)/2 = 12,8 (примерно)