Question

Решите неравенство: корень 4-ой степени из x + 1 > 30/x

Answer 1

ОДЗ:

{х+1 ≥0⇒х≥-1

{x≠0

При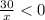 $\frac{30}{x}$  неравенство верно при любом х из ОДЗ

x∈[-1;0) - решение неравенства

При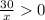  $\frac{30}{x}0$ , т.е при x>0 возводим обе части неравенства в четвертую степень:

$x+1 (\frac{30}{x})^4$

Решаем  неравенство графически:

См. рис.

Строим графики y=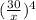$(\frac{30}{x})^4$ ( красного цвета)

$y`=-\frac{4\cdot30^4}{x^5}$

при x >0

кривая убывает.

Строим y=x+1 это прямая синего цвета, возрастает на (-∞;+∞)

Кривая и прямая пересекаются в одной точке, это х=15

Поэтому неравенство верно  при x > 15

О т в е т. [-1;0) U (15;+∞)

Answer 2

ответ и Объяснение:

в приложении