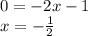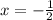Прям ! представьте в виде дроби выражение ответ по идее (так написано в приложении) нужно решать методом покоэффициентного равенства многочленов (поочередное сложение нескольких слагаемых), но мне все равно, главное что бы было решение и ответ, который сходится! !



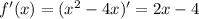
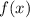 , в которой проведена касательная. Это
, в которой проведена касательная. Это 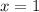 точки М. Подставим в производную, чтобы найти наклон этой касательной.
точки М. Подставим в производную, чтобы найти наклон этой касательной.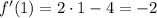
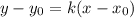
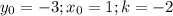
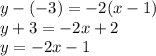
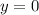 . То есть,
. То есть,