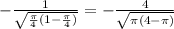1. f'(x)=(х²+х⁴-3х³+2)'=2x+4x³-6x f'(0)=0
2. f'(x)=(2*(2x+3)-2*(2x-1))/(2x+3)²=8/(2x+3)²; f'(2)=8/(7)²=7/49
3. f'(x)=2х*е²ˣ+х²*2е²ˣ=2хе²ˣ*(1+х)
4. f'(x)=2х/(х²+4)
5. f'(x)=-8cosxsinx=-4sin2x
6. f'(x)=(-1/(√(1-x))*(1/2√x); f'(π/4)=(-1/√1-π/4)*(1/2*((√π)/2)))=
(-1/√1-π/4)*(1/2*((√π)/2)))=-√π√(4-π)/π√π=-√(4-π)/π.
Любое выражение в квадрате принимает наименьшее значение 0. Сумма квадратов тоже принимает наименьшее значение 0.
Следовательно, наименьшее значение выражения 0. Чтобы выражение было равно 0, нужно, чтобы либо первое слагаемое было х, а второе -х; либо первое слагаемое -х, а второе х; либо оба слагаемых должны быть равны 0. Так как здесь сумма квадратов, то ни одно из слагаемых отрицательным быть не может => Оба слагаемых равны 0.
5х+4у+6=0 3х+4у+2=0
Выражаем 4у из обоих уравнений:
4у=-6-5х 4у=-2-3х
Приравниваем -6-5х=-2-3х
-2х=4
х=-2
Подставляем х в одно из уравнений:
4у=-2-3*(-2)
4у=4
у=1
1)f'(x)=2x+4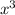 -9
-9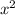
f'(0)=0
2)f'(x)=
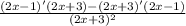 =
=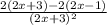 =
=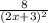
f'(2)=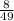
3)f'(x)=(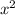 )'
)'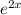 +(
+(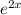 )'
)'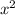 =2x
=2x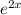 +2
+2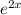
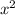 =
=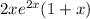
4)f'(x)=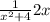
5)f'(x)=4*2cosx(-sinx)=-4sin(2x)
6)f'(x)=
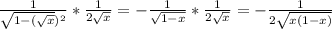
f'(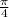 =
=