б) если рассмотреть равенство: x² + (y+1)² = 4
то график этого уравнения --это окружность с центром в (0; -1) радиуса 2.
уравнение окружности с центром (x₀; y₀) радиуса R: (х-х₀)² + (y-y₀)² = R²
в задании знак неравенства "больше", т.е. это часть плоскости ВНЕ круга, включая границу (окружность)
например: точка (2;-3)
2² + (-3+1)² ≥ 4 верно...
а) неравенство с модулем со знаком "меньше" равносильно двойному неравенству: -2 < y-x-1 < 2 (прибавим 1)
-1 < y-x < 3
двойное неравенство равносильно системе неравенств (пересечению промежутков):
{y-x<3
{y-x>-1
или
{ y < x+3 (часть плоскости НИЖЕ (знак "<") прямой у=х+3)
{ y > x-1 (часть плоскости ВЫШЕ (знак ">") прямой у=x-1)
это полоса между параллельными прямыми...
и всегда можно проверить...
например, точка (2;-1) не принадлежит этому множеству...
|-1-2-1| < 2 неверно
точка (0;0) принадлежит этому множеству...
|0-0-1| < 2 верно
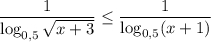
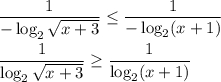
Пусть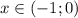 
. Тогда левый логарифм положителен, а правый отрицателен. Если мы домножим обе части неравенства на произведение логарифмов, неравенство сменит знак:
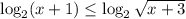
Логарифм с основанием, большим единицы, — монотонно возрастающая функция, поэтому:
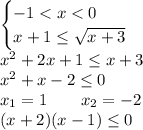
Методом интервалов получим, что ![x \in [-2;1]](/tpl/images/4978/0209/a3a78.png)
. Объединяя с первым условием, получим: .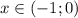
Пусть теперь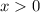 
. Тогда, когда мы умножим обе части неравенства на произведение логарифмов, неравенство сохранит знак:
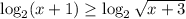
Проделываем всё то же самое:
![\begin{cases}x 0\\ x+1 \ge \sqrt{x+3}\end{cases}\\x^2+2x+1 \ge x+3\\x^2+x-2\ge 0\\(x+2)(x-1) \ge 0\\x \in (-\infty; -2] \cup[1;+\infty)](/tpl/images/4978/0209/534f4.png)
Подходит только правый интервал:
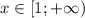
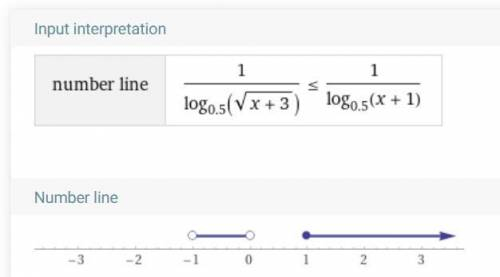
ответ: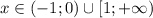 
На скриншоте проверка на компьютере.
Если что-нибудь непонятно — спрашивай.
1) х1+х2=-b/a
x1=x2+8
x2+x2+8=12
2*x2=4
x2=2 x1=10
x1*x2=c/a
20=m
2)
(x1+x2)^2-2*x1*x2=10
16-2*x1*x2=10
-2*x1*x2=-6
x1*x2=3
x1*x2=c/a
p=3