Примем за 1 - объем цистерны
Пусть t цис./ч - производительность "медленного" насоса.
Тогда 3t цис./ч - производительность "быстрого" насоса.
(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.
(t+3t)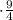 - объем работы системы из двух насосов за 2ч 15мин.
- объем работы системы из двух насосов за 2ч 15мин.
Получим уравнение: 
9t = 1

Значит, 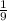 - цис./ч - производительность "медленного" насоса.
- цис./ч - производительность "медленного" насоса.
Тогда 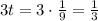 - цис./ч - производительность "быстрого" насоса.
- цис./ч - производительность "быстрого" насоса.
Следовательно, 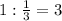 ч - потребуется "быстрому" насосу на заполнение цистерны.
ч - потребуется "быстрому" насосу на заполнение цистерны.
ответ: 3 ч.

5(а-b)-4(2a-3b) = 5a-5b-8a+12b = 7b-3a
-2(3x-2y)-5(2y-3x) = -6x+4y-10y+15x = 9x-6y
7(4p+3)-6(5+7p) = 28p+21-30-42p=-14p-9
(x^2-1)*3x-(x^2-2)*2x = 3x^3-3x-2x^3+4x = x^3+x
(4a^2-3b)*2b-(3a^2-4b)*3b=8a^2 b - 6b^2 - 9a^2 b+12b^2= -a^2 b + 6b^2