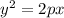ее фокус находится в точке с координатами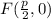 
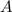находиться в системе уравнения 
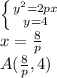Если уравнение касательной равна 
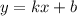с учетом того что она проходит через точку 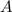получаем 
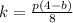, подставляя 
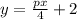
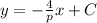он проходит через точку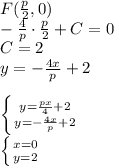 
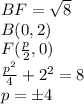
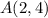
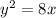
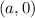центр окружности (так как центр лежит на оси 
) 
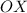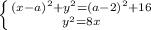
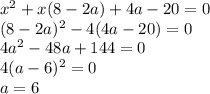
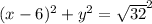
у=15х-21
у=7х-77
15х-21=7х-77
15х-21-7х+77=0
8х=-56
х=-7
Подставляем в любое уравнение х=-7
у=15*(-7)-21
у=-126
Точка пересечения имеет координаты (-7;-126)