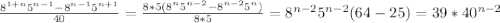
Объяснение:
Квадратное уравнение имеет вид ax²+bx+c=0.
a, b и c - коэффициенты уравнения.
9) Найдите произведение корней уравнения:
х(х – 2) + (х – 1)(х – 2) – 5(2 - x) = 0 ;
x²-2x+x²-3x+2-10+5x=0;
2x²-8=0;
x²-4=0;
Данное уравнение неполное: а=1; b=0; c=-4.
Произведение корней квадратного уравнения равно свободному члену уравнения - с.
В данном уравнении с=-4. Значит x1*x2=-4. x1=2; x2=-2.
Проверим:
x²=4;
x1,2=±2. Всё точно!
***
10) Найдите сумму корней уравнения:
х² (х² – 6х + 9) – 4(x² — 6х + 9) = (0) ; Раскроем скобки и приведем подобные слагаемые:
x^4-6x³+9x²-4x²+24x-36=0;
x^4 - 6x^3 + 5x² + 24x - 36=0;
Вероятно в задании ошибка. Уравнение 4 степени в школе не проходят.
с решением