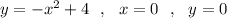
Если задано х=0, то непонятно, площадь какой области находить, слева или справа от прямой х=0. Если задано х>0 , то тогда это правая область, если х<0 , то тогда это левая область . Если вообще не было бы написано уравнение х=0, то эта область находится под параболой до оси ОХ (у=0) .
Найдём площадь правой области при условии х>0 . Если нужна площадь левой области, то она такая же, как и площадь правой области в силу симметрии криволинейной трапеции . Если нужна площадь всей области между параболой и осью ОХ , то она равна удвоенной площади правой области .
Точки пересечения:
Делаем диагональное сечение и находим боковое ребро.
В сечении - трапеция с основаниями как диагонали квадратов оснований пирамиды √2 и 4√2. Высот задана: Н = 3 см.
Тогда боковое ребро L = √(3² + ((1.5√2)²) = √(9 + (9/2)) = √(27/2) = 3√3/2.
Отсюда находим высоту h боковой грани (она же и апофема А):
А = h = √(L² - ((4-1)/2)²) = √((27/2) - (9/4)) = √45/2 = 3√5/2.
Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.
Sбок =( (4*1 + 4*4)/2)*(3√5/2) = 15√5 см².
Площадь оснований So = 1*1 + 4*4 = 17 см².
Полная поверхность равна их сумме.
- 11 - 1 < 2X - 4X - 5X ≤ 13 - 1
- 12 < - 7X ≤ 12
- 12/7 < - X ≤ 1
1 ( 5/7 ) > X ≥ - 1
X ∈ [ - 1 ; 1 ( 5/7 ) )
2A^2 + B^2 + C^2 ≥ 2A * ( B + C )
2A^2 ≥ 2AB + 2AC - B^2 - C^2
2A^2 ≥ ( 2AB - B^2 ) + ( 2AC - C^2 )
2A^2 ≥ B * ( 2A - B ) + C * ( 2A - C )