(-1)¹¹-(-1)¹¹=-1+1=0
-(-1)⁴-(-1)²-(-1)²=-1-1-1=-3
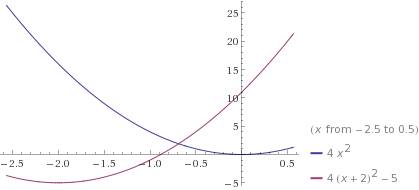
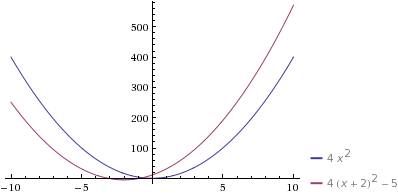
если для первого графика y = 4x^2 вершина находится в точке (0;0), то
ось симметрии параболы - ось OY (уравнение x=0)
то для второго графика ось симметрии сместится влево на 2 (уравнение x = -2, все первое слагаемое обратится в 0 и получится y = -5), т.е. для второго графика вершина опустится вниз по оси OY на 5 единиц и сместится влево на 2 единицы по оси OX
координаты вершины новой параболы (-2;-5), ветви вверх и она в точности повторяет первый график (из новой точки---новой вершины), иными словами
новый график получится параллельным переносом исходного графика вниз по оси OY на 5 единиц и влево по оси OX на 2 единицы
-1 в четной степени равно 1
-1 в нечетной степени равно -1
(-1)в 11 степени - (-1) в 11 степени =-1-(-1)=0
(-1)в 4 степени - (-1)во 2 степени - (-1) во 2 степени =1-1-1=-1