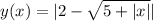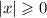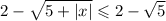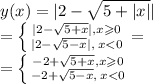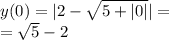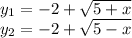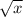16. Острый угол - угол меньше 90 градусов
Тупой угол - угол больше 90 градусов
Прямой угол - угол равный 90 градусов
17. Вертикальными называются углы, образованные при пересечении двух прямых и лежащие против друг друга.
Вертикальные углы равны
19. Прямые перпендикулярность, если при пересечении образуют прямые углы
20. Две прямые, лежащие в одной плоскости, перпендикулярные третьей параллельны, поэтому никогда не пересекутся
21. Приборы для построения и измерения углов на местности называются эккер и теодолит