1. те выражения, которые можно , воспользовавшись распределительным законом: 1)а) 2m-4m+5n б)3m-2n в) - id334614520210625 от анарка3 25.06.2021 01:32

Question

Алгебра: 1. те выражения, которые можно , воспользовавшись распределительным законом: 1)а) 2m-4m+5n б)3m-2n в) -1,3a+4a-3,7a г) 4x-8y-6x+11y 2)a) -7x-8x+2x б) -1,5a+7,3b в) 1,8b-5,8b+3b г) -2m+3n-8m-n 2. выражение: 1)а) (a-2)+(a-+7) б) 2•(а-+6) в) -3•(2x-9)+(-5x+1) 2) a) (x-3)+(x--3x) б) -2•(m--5) в) 4•(2a-1)+(7-5a)

анарка3 · Accepted Answer

Tg 6x*cos 2x - sin 2x - 2sin 4x = 0
Замена 2x = y
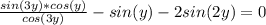
$\frac{sin(3y)*cos(y)}{cos(3y)} - sin(y) - 2sin(2y) = 0$
Найдем функции тройного аргумента
sin 3y = sin(y + 2y) = sin y*cos 2y + cos y*sin 2y =
= sin y*(1 - 2sin^2 y) + cos y*2sin y*cos y =
= sin y*(1 - 2sin^2 y) + 2sin y*(1 - sin^2 y) =
= sin y*(1 - 2sin^2 y + 2 - 2sin^2 y) = sin y*(3 - 4sin^2 y)
Аналогично cos 3y = cos y*(4cos^2 y - 3)
Получаем
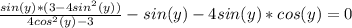
$\frac{sin(y)*(3 - 4sin^2(y))}{4cos^2(y) - 3} - sin(y) - 4sin(y)*cos(y) = 0$
Выносим sin y за скобки.
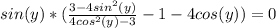
$sin(y)*(\frac{3 - 4sin^2(y)}{4cos^2(y) - 3} - 1 - 4cos(y)) = 0$
Умножаем всё на 4cos^2 y - 3
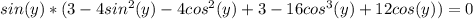
sin(y)*(3-4sin^2(y) - 4cos^2(y)+3-16cos^3(y)+12cos(y))=0

sin(y)*(3-4sin^2(y) - 4cos^2(y)+3-16cos^3(y)+12cos(y))=0

Приводим подобные
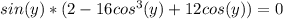
sin(y)*(2-16cos^3(y)+12cos(y))=0

1) sin y = sin 2x = 0; 2x = pi*k; x = pi/2*k
2) Кубическое уравнение делим на -2
8cos^3 y - 6cos y - 1 = 0
2cos y(4cos^2 y - 3) = 1
2cos 3y = 1
cos 3y = 1/2
3y = 6x = +-pi/3 + 2pi*n
x2 = +-pi/18 + pi/3*n
ответ: x1 = pi/2*k; x2 = +-pi/18 + pi/3*n

MOGZ ответил