1. 18xy
2. 10a²
3. -2a²
4. (xyz)²
Объяснение:
Одночлены - это алгебраическое выражение, являющееся произведением чисел, переменных и их степеней.
1. Сначала: надо перемножить числовую часть (коэффициент), а затем буквенную, т.е. 3×6=18 и х•у=ху, и затем соединим числовую и буквенную части - 18ху.
2. Тут остаётся как есть, т.к. переменная одна и она просто перемножается на коэффициент.
3. Тут остаётся как есть, т.к. переменная одна и просто перемножается на коэффициент.
4. Здесь надо все переменные возвести во вторую степень.

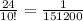

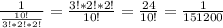
F(-x)=(-x)³+(-x)⁵-6=-x³-x⁵-6=-(x³+x⁵+6)
F(x)≠-F(-x) - функция ни какая.