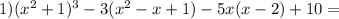
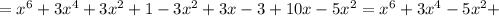
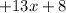
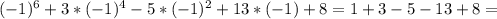
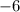
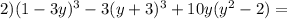
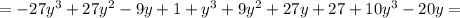
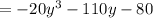
Если одночлены состоят из одинаковых переменных в одинаковых степенях, то они являютсяподобными. Коэффициенты одночленов при этом могут различаться. Примеры подобных одночленов:
3a2 и –4a2; 31 и 45; a2bx4 и 1,4a2bx4; 100y3и 100y3
Но одночлены –6ab2 и 6ab не являются подобными, так как у них переменная b находится в разных степенях.
Подобные одночлены обладают удивительным свойством — их можно легко складывать и вычитать. Если нужно найти сумму двух или более подобных одночленов, то их коэффициенты надо сложить, а переменные в сумме оставить без изменений. Если же требуется найти разность двух подобных одночленов, то коэффициент одного одночлена надо вычесть из второго, а переменные оставить без изменений. Примеры:
4x2 + 15x2 = 19x2
5ab – 1,7ab = 3,3ab
13a10b5c3 – 13a10b5c3 = 0a10b5c3 = 0
Эти действия называются приведением подобных одночленов.
Почему же подобные одночлены можно так складывать и вычитать? Попробуем упростить выражения, не используя правила приведения подобных одночленов:
2x + 4x = (x + x) + (x + x + x + x) = x + x + x + x + x + x = 6 * x = 6x
2x – 4x = (x + x) – (x + x + x + x) = x + x – x – x – x – x = – x – x = – (x + x) = –(2x) = –2x
То есть свойство подобных членов вытекает из правила арифметики о том, что произведение двух чисел является ничем иным как суммой из слагаемых одного числа, где количество слагаемых равно другому числу:
2 * 3 = 3 + 3 = 2 + 2 + 2
при x= -1
(1+1)³-3·(1+1+1)²-5·(-1)·(-1-2)+10=8-27-15+10=-24
2) (1-3y)³ - 3(y+3)³+10y(y²-2)
при y= 2
(1-6)³-3·5³+10·2·(4-2)=-125-3·125+40=-500+40=-460