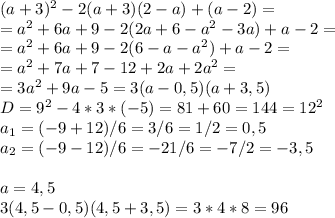
точно не знаю, но 4 вроде так
Воспользуемся теоремой Виета, которая гласит, что в квадратном уравнении вида х^2 + bх + с = 0 действует следующее правило: х1+х2=-b (в данном случае b1=-7) х1*х2=с (в данном случае с1=-1) Решение: новое уравнение будет выглядеть так: х^2 + (b2)*х + с2 = 0 найдём b2 и с2: По теореме Виета: Во-первых: 5*х1 + 5*х2 = -b2 = = 5*(х1+х2) = -5*b1 = -5*(-7) = 35 = -b2 следовательно b2= -35 во-вторых: (5*х1)*(5*х2)=с2 25*(х1*х2) = с2 25*с1 = с2 = 25*(-1) = -25 Подставляем в новое уравнение найденные b2 и с2: ответ: х^2-35х-25=0
1) ответ : x1 = 0 , x2 = 1
2) ответ : x1 = 1 , x2 = -0,5
Объяснение:
1) x^2 / x+3 - x / x+3 = 0
т.к знаменатели у нас одинаковые,то мы можем записать одной дробью
x^2-x / x+3 = 0
ОДЗ : x+3 ≠ 0
x ≠ -3
мы знаем,что дробь равна нулю тогда,когда числитель равен нулю
x^2 - x = 0
x^2 = x
x1 = 0
x2 = 1
ответ : x1 = 0 , x2 = 1
3) x+2 / x - 5x+1 / x+1 = 0
первую дробь домножим на x+1 , вторую дробь на x
( (x+2)*(x+1) - (5x + 1)*x ) / x(x+1) = 0
ОДЗ : x(x+1) ≠ 0
x ≠ 0 и x ≠ -1
теперь выполняем умножения
( x^2 + x + 2x + 2 - 5x^2 - x ) / x(x+1) = 0
приравниванием числитель к нулю
x^2 + x + 2x + 2 - 5x^2 - x = 0
считаем
- 4x^2 + 2x + 2 = 0 (*-1)
4x^2 - 2x - 2 = 0
D : (-2)^2 - 4*4*(-2) = 4 + 32 + 36(6)
x1 = (2 + 6) / 2*4 = 8 / 8 = 1
x2 = (2 - 6) / 2*4 = -4 / 8 = - 1/2 = -0,5
ответ : x1 = 1 , x2 = -0,5