катер плыл сначала 30 минут против течения реки, а затем 15 минут по озеру в отсутствии течения. найдите скорость течения реки(км/ч).если собственная скорость катера постоянна и равна 20 км/час, а средняя скорость его движения за весь промежуток времени составила 17 км
x - скорость течения реки
0,5 (20-x ) - путь, пройденный катером против течения реки,
0,25·20=5 - путь, пройденный катером по озеру
(0,5+0,25) - время, которое катер был в пути.
(0,5 (20-x ) + 5)/ (0,5+0,25) = 17 - средняя скорость катера
(10-0,5x+5)/(0,75)=17
(15-0,5x)=17·3/4
60-2x=51 x=9/2 x=4,5
Сделаем замену сначала: 7x=t, т.е 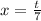
Поскольку x->0, то и 7x->0, значит и t->0.
Подставляем в наш предел то что получилось с учетом замены:
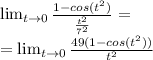
Поскольку нас неопределенность 0/0 можно использовать правило Лопиталя.
Получаем:
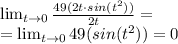
Возможно я не так понял задание и там имелось в виду:
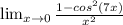
Тогда используем ту же самую замену.:
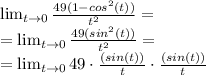
Видим что здесь произведение двух "первых замечательных пределов", а именно:
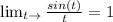
Используем этот факт и получим: 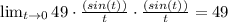
Как-то так. Но обязательно проверь.
Пусть Х - часть окружности, которую первое тело преодолевает за 1 минуту, а Y - часть окружности, которую за одну минуту преодолевает второе тело.
Получаем систему уравнений
X + Y = 1/2 X = 0,3
X - Y = 1/10 , откуда Y = 0,2
Итак, первое тело за минуту преодолевает 0,3 окружности, а второе тело 0,2 окружности. Следовательно, второе тело проходит окружность за 5 минут, а первое тело за 3 минуты 20 секунд, то есть на 100 секунд быстрее второго.