1.представьте в виде многочлена: а)(x-4)(x+2) б)(4a-b)(2a+3b) в)(y-5)(y^2-2y+3) 2.разложите на множители: а)a(x-y)+4(x-y) б)3x-3y+ax-ay 3. выражение: (x+y)y-(x^3-y)(y-1) 4.докажите тождество: (y-a)(y-b)=y^2-(a+b)y+ab 5.периметр прямоугольника равен 40 см, если его длину уменьшить на 3 см а ширину увеличить на 6 см .то его площадь увеличится на 3 см^2.определите площадь первоначального прямоугольника.
a)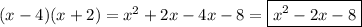
б)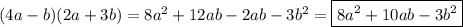
в)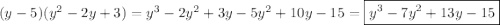
#2а)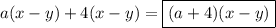
б)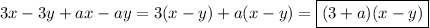
#3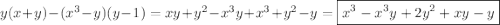
#4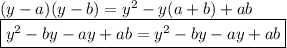
#5ответ: