1. (х+4)(х+6) 2. (х -3)(х -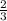 
)
Объяснение:
1. х^2 +10x - 24
a=1, b=10, c=-24
Находим дискриминант и получаем D= 4
формулы x1 =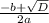 
находим первый корень, который равен -4
А с формулы х2=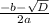
находим второй корень, который равен -6
Используем формулу квадратного трёхчлена ax^2+bx+c=a(x-x1)(x-x2)
Получаем:
x^2+10x-24= 1(x-(-4))(x-(-6)) = (x+4)(x+6)
2. 3x^2-11x+6
a=3, b=-11, c=6
Находим дискриминант и получаем D= 49
формулы x1 = 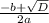находим первый корень, который равен 3
А с формулы х2=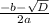 находим второй корень, который равен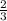
Используем формулу квадратного трёхчлена ax^2+bx+c=a(x-x1)(x-x2)
Получаем:
3x^2-11x+6= 1(x-3)(x- )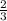
1. (х+4)(х+6) 2. (х -3)(х - )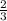
Объяснение:
1. х^2 +10x - 24
a=1, b=10, c=-24
Находим дискриминант и получаем D= 4
формулы x1 = 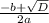находим первый корень, который равен -4
А с формулы х2=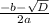 находим второй корень, который равен -6
Используем формулу квадратного трёхчлена ax^2+bx+c=a(x-x1)(x-x2)
Получаем:
x^2+10x-24= 1(x-(-4))(x-(-6)) = (x+4)(x+6)
2. 3x^2-11x+6
a=3, b=-11, c=6
Находим дискриминант и получаем D= 49
формулы x1 = 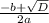находим первый корень, который равен 3
А с формулы х2=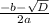 находим второй корень, который равен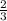
Используем формулу квадратного трёхчлена ax^2+bx+c=a(x-x1)(x-x2)
Получаем:
3x^2-11x+6= 1(x-3)(x- )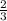
Второй множитель по основному тригонометрическому тождеству всегда равен 1, первый равен косинусу двойного угла по соответствующей формуле. Значит, цепочку равенств можно продолжить: