Объяснение:
1. 4x²-3x=3(12-x)
4x²-3x-36+3x=0
4x²+0·x+(-36)=0, где
a=4 - старший коэффициент;
b=0 - второй коэффициент;
c=-36 - свободный член.
2. a) -12x²+6x+5=0, числовые коэффициенты a,b,c≠0⇒полное квадратное уравнение;
b) x²=6x; x²-6x+0=0, где c=0⇒неполное квадратное уравнение;
c) -x²-6x+15=0, где a,b,c≠0⇒полное квадратное уравнение;
d) 8x²-9x+1=0, где a,b,c≠0⇒полное квадратное уравнение;
e) 3x+4=-2x²; 2x²+3x+4=0, где a,b,c≠0⇒полное квадратное уравнение.
ответ: вариант B.
3. x²-4x+c=0
a) D=b²-4ac; 0=(-4)²-4·1·c; 0=16-4c; 4c=16; c=16/4=4
b) D=0; x₁=(4-√0)/2=2; x₂=(4+√0)/2=2
4. x²-9x-17=0
По формуле Виета:
x₁+x₂=9
x₁·x₂=-17
x₁²+x₂²=(x₁+x₂)²-2x₁x₂=9²-2·(-17)=81+34=115
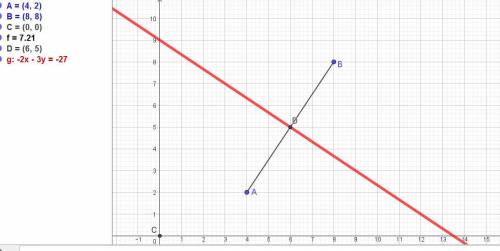
Прямая,все точки которой находятся на равных расстояниях от точек A(4;2) и B(8;8), это перпендикуляр к середине отрезка АВ.
Уравнение АВ: (х - 4)/(8 - 4) =(у - 2)/(8 - 2).
(х - 4)/4 =(у - 2)/6) или (х - 4)/2 =(у - 2)/3.
Или в общем виде Ах + Ву + С = 0.
3х - 12 = 2у - 8,
3х - 2у - 4 = 0. Здесь А = 3, В = -2.
Перпендикулярная прямая имеет вид -Вх + Ау + С1 = 0.
Для определения коэффициента С1 надо подставить координаты точки, принадлежащей этой прямой.
Такая точка - середина АВ (точка Д).
Д = (1/2)(A(4;2) + B(8;8))/2 = (6; 5). Подставляем:
2*6 + 3*5 + С1 = 0,
С1 = -12 - 15 = -27.
ответ: уравнение прямой, все точки которой находятся на равных расстояниях от точек A(4;2) и B(8;8), это 2х + 3у - 27 = 0.
Воспользуемся умножением неравенств
3.3<sqrt(11)<3.4
16.5<5sqrt(11)<17 (умножаем на 5)
-6.6>-2sqrt(11)>-6.8 (умножаем на -2 и соответственно меняем знаки неравенств)