(-1,5;2,5) (2;-1) (-2;1) (1,5;-2,5)
Объяснение:
{x²+2xy+y²=1 {(x+y)²=1 {x+y=-1 {x+y=1
{x²-xy=6 ⇔ {x²-xy=6 ⇔ {x²-xy=6 ⇔ {x²-xy=6
{y=-1-x { y=1-x
{x²-x(-1-x)=6 {x²-x(1-x)=6
x²+x+x²-6=0 x²-x+x²-6=0
2x²+x-6=0 2x²-x-6=0
D=1²-4·2·(-6)=49 D=(-1)²-4·2·(-6)=49
x₁=(-1-7)/4=-2 y₁=-1-(-2)=1 x₁=(1-7)/4=-1,5 y₁=1-(-1,5)=2,5
x₂=(-1+7)/4=1,5 y₂=-1-1,5=-2,5 x₂=(1+7)/4=2 y₂=1-2=-1
Объяснение:
Задание 1
у=х²-4х-5
а)у(2)=2²-4*2-5=4-8-5=-9
б) у=3 х²-4х-5=3
х²-4х-8=0 , Д=в²-4ас, Д=(-4)²-4*1*(-5)=16+20=36
х₁=(-в+√Д):2а , х₁=(4+6):2=5
х₂=(-в-√Д):2а , х₂=(4-6):2=-1 .
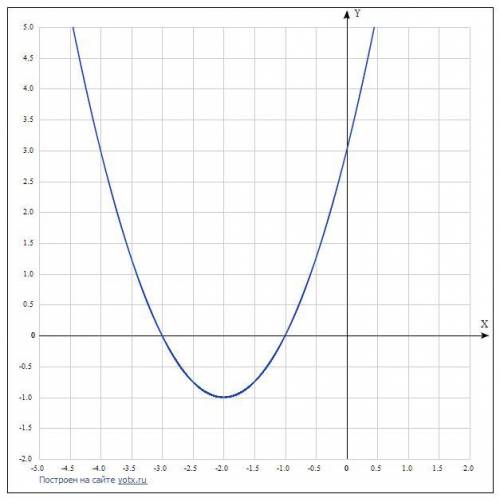
Задание 3
у=х²+4х+3
Это парабола ,ветви вверх.
а)х₀=-в/2а, х₀=(-4)/2=-2 , у₀=(-2)²+4*(-2)+3 =-1 , (-2; -1).
б) х=-2
в)Точки пересечения с осью ох, т.е у=0
х²+4х+3=0
Д=в²-4ас, Д=4²-4*1*3=16+12=48=4
х₁=(-в+√Д):2а , х₁=(-4+2):2 , х₁=-1 , (-1;0)
х₂=(-в-√Д):2а , х₂=(-4-2):2 , х₂=-3 , (-3;0)
Точки пересечения с осью оу, т.е. х=0, у=3 (0; 3)
Доп.точки у=х²+4х+3 :
х: -5 -4 -3 1
у: 8 3 0 8
д) возрастает при х>-2
убывает при х<-2
е) у>0 при x<-2 , х>-1