




1) x ∈ ∅ ⇔ разложить на множители не получится.
2) x ∈ ∅ ⇔ разложить на множители не получится.
3) 9x² + 6x + 1 = (3x + 1)²
Объяснение:
Во всех примерах будем пользоваться формулой:
ax² + bx + c = a(x - x₁)(x -x₂)
Для этого необходимо найти корни каждого выражения.
1) x²-2x+12
x² - 2x + 12 = 0

D < 0 ⇒ нет корней
x ∈ ∅ ⇔ разложить на множители не получится.
2) x²+x+20
x² + x + 20 = 0
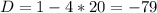
D < 0 ⇒ значит нет корней
x ∈ ∅ ⇔ разложить на множители не получится.
3) 9x²+6x+1
9x² + 6x + 1 = 0

x = 
9x²+6x+1 = 9(x + 1/3)² = (3x + 1)²
(t+1)(t-3)>=5, значит: t^2-2t-8=0. D=4+32=36. t1=(2+6)/2=4, t2=-2. (t+2)(t-4)>=0. Получили, что t принадлежит от минус бесконечности до минус двух и от четырех до плюс бесконечности. Обратная замена дает два случая: ПЕРВЫЙ: x^2+3x<=-2, тогда: x^2+3x+2<=0, угадывая корни по теореме Виета имеем: (x+1)(x+2)<=0, тогда: х принадлежит отрезку [-2; -1]. ВТОРОЙ: x^2+3x>=4, значит: x^2+3x-4>=0, угадав корни имеем: (x+4)(x-1)>=0, тогда х принадлежит от минус бесконечности до минус 4 включительно и от единицы включительно до плюс бесконечности. ОТВЕТ: х принадлежит (минус бесконечность; -4] U [-2;-1] U [1; плюс бесконечность).