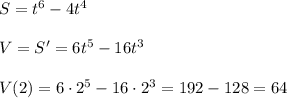
3265920
Объяснение:
ответ предыдущего пользователя Formik правильный, но возможно кому-то будет проще решать через перестановки, то
1) Можно просто отнять от числа всех возможных перестановок из 10 элементов по 10, то есть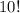 
, число перестановок, когда 0 стоит на первом месте, то есть 
.
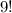Имеем: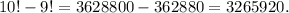 
2) Чтобы понять лучше, почему именно 9!, давайте продемонстрируем это на 4 числах. К примеру, у нас есть числа 0, 1, 2, 3. Нас просят найти сколько таких перестановок может быть, если числа (1) не повторяются и (2) различаются друг от друга порядком их размещения. Мы также помним, что число 0 не может стоять на первом месте. Давайте подумаем как 0 может стоять на первом месте:
0123, 0132, 0231, 0213, 0312, 0321. - Всего 6 перестановок. Но вдумайтесь: мы ищем только те перестановки, КОТОРЫЕ ПОСЛЕ 0, так как 0 стоит на первом месте, мы его не меняем вместе с остальными цифрами! Это нужно понять.
Поэтому, от числа всех перестановок, которые могли бы быть, это 4!, мы должны отнять все те перестановки, когда 0 стоит на первом месте, это 3!, так как меняем мы 3 цифры после 0! И выходит у нас: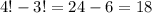 
разместить все цифры так, чтобы 0 не стоял на первом месте! (см. ниже фото)
3) Аналогично делаем когда у нас 10 цифр: мы просто находим перестановки цифр, которые после 0 - это 9!, от числа всех перестановок, которые могли бы быть вообще, если бы не было условия, что 0 не может стоять не первом месте - это 10!
Целые числа называются взаимно простыми, если они не имеют никаких общих делителей, кроме ±1. Примеры: 14 и 25 взаимно просты, а 15 и 25 не взаимно просты (у них имеется общий делитель 5).
Наглядное представление: если на плоскости построить «лес», установив на точки с целыми координатами «деревья» нулевой толщины, то из начала координат видны только деревья, координаты которых взаимно просты.
8, 15 — не простые, но взаимно простые.
6, 8, 9 — взаимно простые числа, но не попарно взаимно простые.
8, 15, 49 — попарно взаимно простые.
