Максимум в точке х = 
(для записи 
)
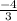Минимум в точке х = -1
Объяснение:
f(x)=2x^3+7x^2+8x+4
Область определения:
Х∈R
f(x)=2x^3+7x^2+8x+4, Х∈R
Определим производную f:
f(x) = 2x^3+7x^2+8x+4
f'(x) = d/dx (2x^3+7x^2+8x+4)
f'(x) = d/dx(2x^3) + d/dx(7x^2) + d/dx(8x) + d/dx(4)
f'(x) = 2*3x^2 + 7*2x+8+0
f'(x) = 6x^2+14x+8
f'(x) = 6x^2+14x+8, Х∈R
Представим f'(x) = 0
0=6x^2+14x+8
Решим ур-е относительно Х
6x^2+14x+8=0 | :2
3x^2+7x+4=0
D=b2-4ac = 7^2-4*3*4 = 1
x1,2= -b+-D/2a = -7+-1/2*3
x1= - 4/3
х2= -1
X∈(-∞;- 4/3)
X∈(- 4/3;-1)
max: - 4/3
min: -1
функция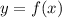 
не существует. То есть найдем такие значения , при которых выражение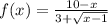 
не имеет смысла. Посмотрели на выражение, подумали и прикинули, что тут может быть где-то два варианта, при которых выражение не имеет смысла:
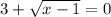, однако понятно, что 
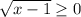, значит знаменатель не обратиться в нуль.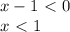
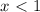функции не существует. То есть она идет от 
и куда-то дальше. Куда — нам пока неизвестно. . Может быть она периодична?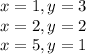 
, при котором числитель обратиться в нуль.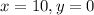 
повставлять разные значения (большие и маленькие).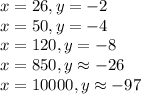 
уменьшается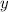 
. Делаем вывод, что функция убывает бесконечно много. То есть 
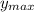— не существует, 
— не существует.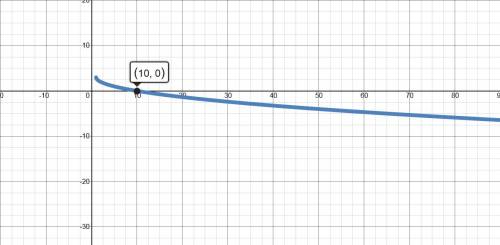 
Объяснение:
f'(x)=(2x^5-4x^3+6x-3)'=5*2x^4-3*4x^2+6=10x^4-7x^2+6