![Найти наибольшее и наименьшее значение функции y=x^3-300x+23 на отрезке [0; 11]](/tpl/images/0383/5024/4d6de.jpg)
Задача: Из A в B одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого авт-ста на 17 км/ч, а вторую половину пути проехал со скоростью 102 км/ч, в результате чего прибыл в В одновременно с первым авт-стом. Найдите скорость первого автомобилиста, если известно, что она больше 65 км/ч.
Обозначим скорость первого автомобилиста за x (км/ч), тогда сорсть второго на первом полупути — ха x−17 (км/ч), на втором полупути — 102 км/ч. Оба проехали общий путь за одно и то же время. Составим и решим уравнение, при условии, что x > 65 (км/ч).
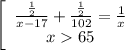
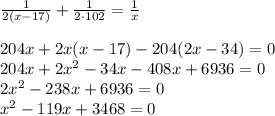
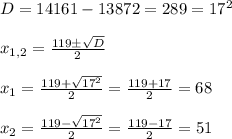
x₂ = 51 < 65 — не удовлетворяет условие
х₁ = 68 > 65 — удовлетворяет условие
ответ: Скорость первого автомобилиста — 68 км/ч.