а) х(х+11)-8>4x
x²+11x-8>4x
x²+11-8-4x>0
x²-4x+3>0
x²-4x+3=0
D=b²-4ac=16-4*3=16-12=4
x1,2=-b±√D/2a
x1=4+2/2=3
x2=4-2/2=1
Розлаживаем множители по формуле
a(x-x1)(x-x2)=(x-3)(x-1)
x∈(-∞;1)∪(3;+∞)
Объяснение:
Сначала просто решим неравенство методом интервалов:
Найдём корни числителя: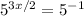 ;
;
3x/2=-1;
x= -2/3;
Найдём корни знаменателя:
x-4=0;
x=4;
Теперь начертим числовую прямую, отметим на ней точки -2/3 и 4 и посмотрим, где всё выражение принимает значения больше нуля (числовая прямая прикреплена).
Мы видим, что всё выражение больше нуля при x>4 и x< -2/3
Поскольку нам нужен наименьшее целое положительное решение, мы берём число 5 (4 мы взять не можем, т.к. в знаменателе будет 0 и потому, что 4 не входит в получившиеся лучи).
ответ: 5.

x=0⇒y=0 ; точка о(0,0) .
x≠ 0 ⇒ 2(y/x)² +5*(y/x) +2 =0;
y/x= -2 ⇒y =- 2x;
y/x= -1/2⇒ y = -1/2*x ;
об'единение графиков y =- 2x и y = -1/2*x (прямых линии)
точка о(0,0) ∈ этим линиям
б) 3y² -10xy +3x²=0;
3(y/x)² -10(y/x) +3 =0;
D/4=5²- 3*3 =16 =4²:
y/x =(5 -4)/3=1/3⇒ y=1/3*x ;
y/x =(5 +4)/3 =3 ⇒y =3*x.
об'единение графиков y = 1/3x и y = 3x (прямых линии)